PBRT-采样前置知识
PBRT-采样前置知识
[TOC]
复数
直角坐标表示
复数的基本单位是$i = \sqrt{-1} $,复数空间的每个数可以表示为$a + bi$的形式,其中,a是实部,b是虚部
复数可以在复平面上表示,复平面的横纵坐标分别为实部和虚部,例如:
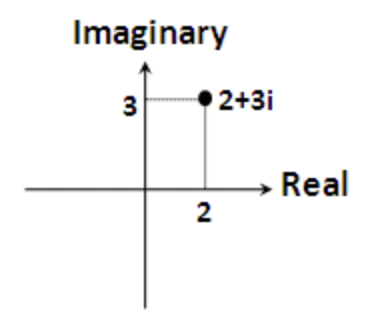
极坐标表示
复数使用极坐标可以表示为$(r, \theta)$,其中$r = \sqrt{a^2 + b^2}$,也称为强度,$\theta = arctan(\frac{b}{a})$,也称为相位
例如,复数$4 + 3i$的直角坐标为$(4, 3)$,极坐标为$(5, arctan(\frac{3}{4}))$
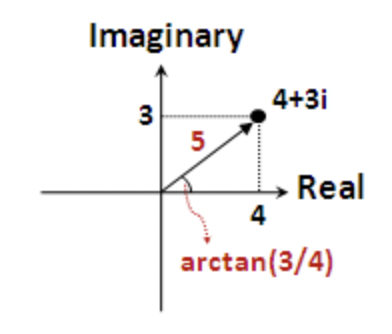
极坐标转直角坐标:
令复数的极坐标为$(r, \theta)$,则直角坐标为$(rcos\theta, rsin\theta)$
复数波和实数波
实数波表示为$cos\theta$和$sin\theta$的形式,复数波使用$e^{i\theta}$表示,且有:
$$
e^{i\theta} = cos\theta + i\ sin\theta
$$
当$\theta = \pi$时,有欧拉公式:
$$
e^{i\pi} = -1
$$
两者的示意图如下:
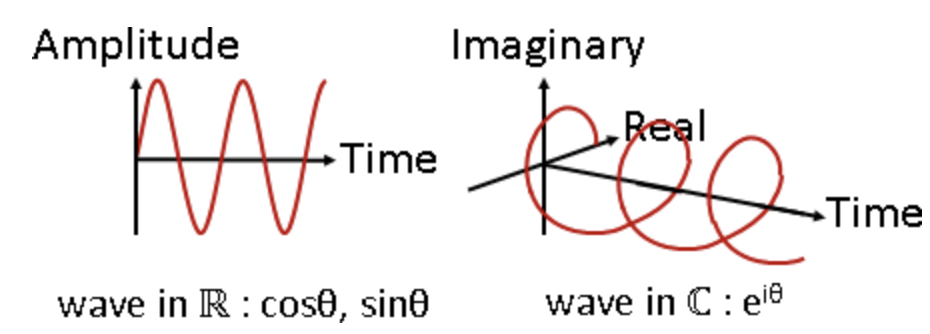
可以通过组合复数波得到实数波:
$$
cos\theta = \frac{e^{i\theta} + e^{-i\theta}}{2} \
sin\theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}
$$
正弦信号
连续时间
$$
x(t) = Acos(w_0t + \phi)
$$
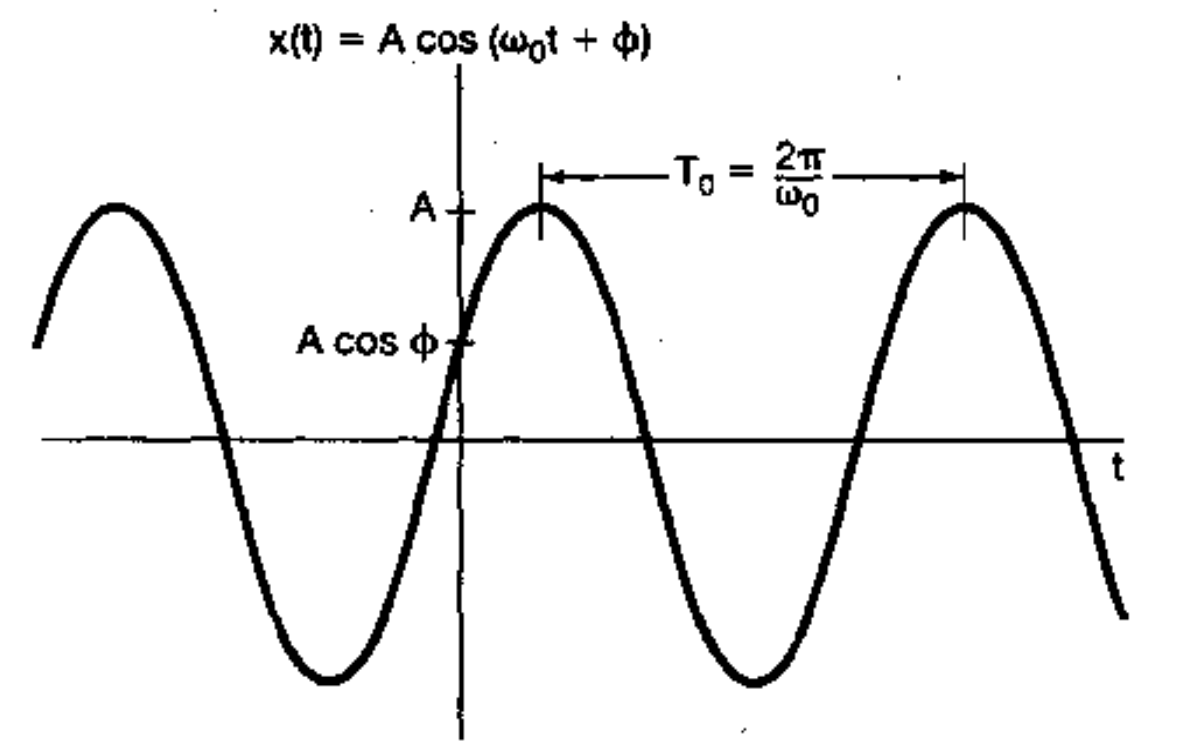
性质
周期性
$$
x(t) = x(t + T_0), period = smallest\ \ T_0
$$
相变和时移等价
$$
Acos[w_0(t + t_0)] = Acos[w_0t + w_0 t_0] \
Acos[w_0(t + t_0) + \phi] = Acos[w_0 t + w_0 t + \phi]
$$
频率不具有周期性
假设有2个信号:
$$
x_1(t) = Acos(w_1 t + \phi) \
x_2(t) = Acos(w_2 t + \phi)
$$
如果$w_1 \neq w_2$,则$x_1(t) \neq x_2(t)$
离散时间
$$
x[n] = Acos(\Omega_0n + \phi)
$$
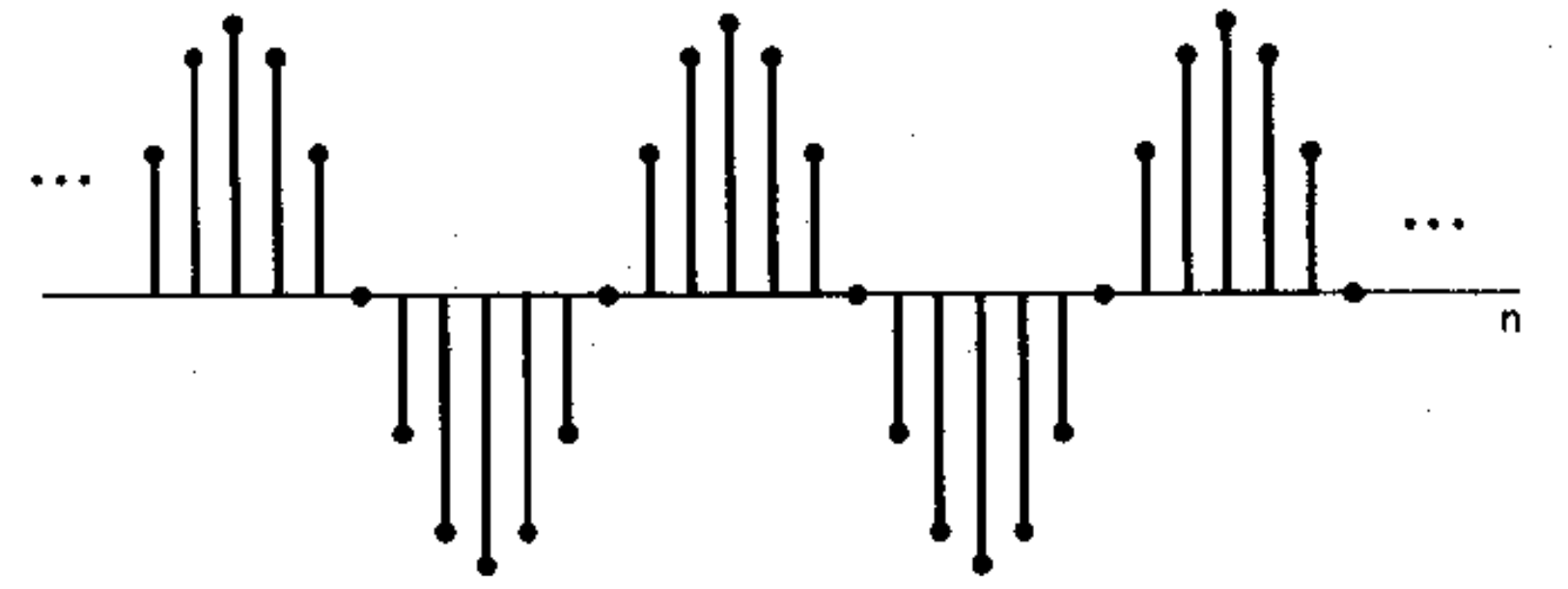
性质
特定条件下具有周期
假设有:
$$
x[n] = x[n + N]
$$
将式子展开:
$$
Acos[\Omega_0 (n + N) + \phi] = Acos[\Omega_0 n + \Omega_0 N + \phi]
$$
如果具有周期性,需要满足:
$$
\Omega_0 N = 2\pi m \
N = \frac{2\pi m}{\Omega_0}
$$
其中$N, m$都是整数,此时周期为最小的$N$
时移等于相变
$$
Acos[\Omega_0(n + n_0)] = Acos[\Omega_0 n + \Omega_0 n_0]
$$
相变不一定等于时移
对于式子:
$$
x[n] = Acos[\Omega_0 n + \phi]
$$
当且仅当$\phi = n_0\Omega_0$时,有:
$$
Acos[\Omega_0 n + \phi] = Acos[\Omega_0(n + n_0)]
$$
否则,相变无法转换成时移
频率具有周期性
假设有两个信号:
$$
x_1[n] = Acos[\Omega_1 n + \phi] \
x_2[n] = Acos[\Omega_2 n + \phi]
$$
当且仅当$\Omega_1 = \Omega_2 + 2\pi m$时,$x_1[n] = x_2[n]$
复指数信号
连续时间
$$
x(t)
= Ce^{at} \
= |C|e^{j\theta} e^{(r+jw_0)t} \
= |C|e^{rt} e^{j(w_0t + \theta)} \
= |C|e^{rt}cos(w_0 t + \theta) + j |C| e^{rt} sin(w_0 t + \theta)
$$
离散时间
$$
x[n]
= C \alpha^n \
= |C|e^{j\theta} (|\alpha| e^{j\Omega_0})^n \
= |C||\alpha |^n e^{j(\Omega_0 n + \theta)} \
= |C||\alpha |^n cos(\Omega_0 n + \theta) + j |C||\alpha |^n sin(\Omega_0 n + \theta)
$$
单位阶跃和单位脉冲函数
离散时间
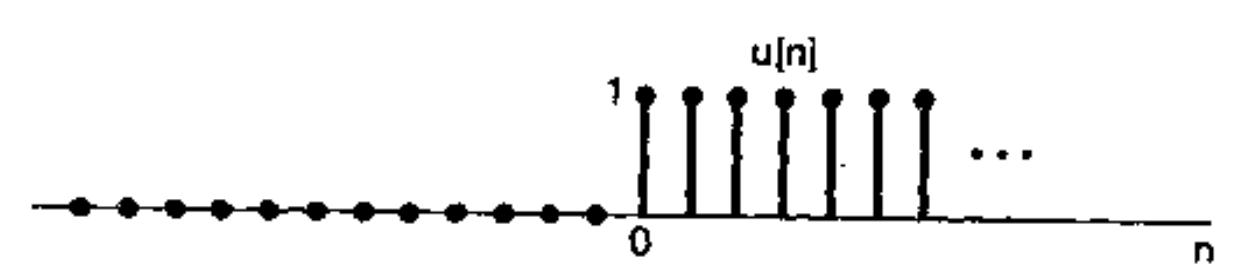
离散时间单位阶跃函数:
$$
u[n] =
\left{
\begin{aligned}
1, & n \geq 0\
0, & n < 0
\end{aligned}
\right.
$$
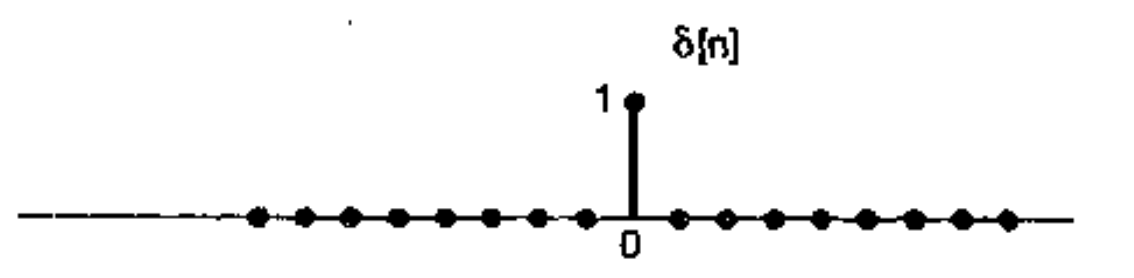
离散时间单位脉冲函数:
$$
\delta[n] =
\left{
\begin{aligned}
1, n = 0 \
0, n \neq 0
\end{aligned}
\right.
$$
关系:
$$
\delta [n] = u[n] - u[n - 1]
$$
$$
u[n]
= \sum_{m = -\infty}^{n} \delta [m] \
= \sum_{k = 0}^{+\infty} \delta[n - k]
$$
连续时间
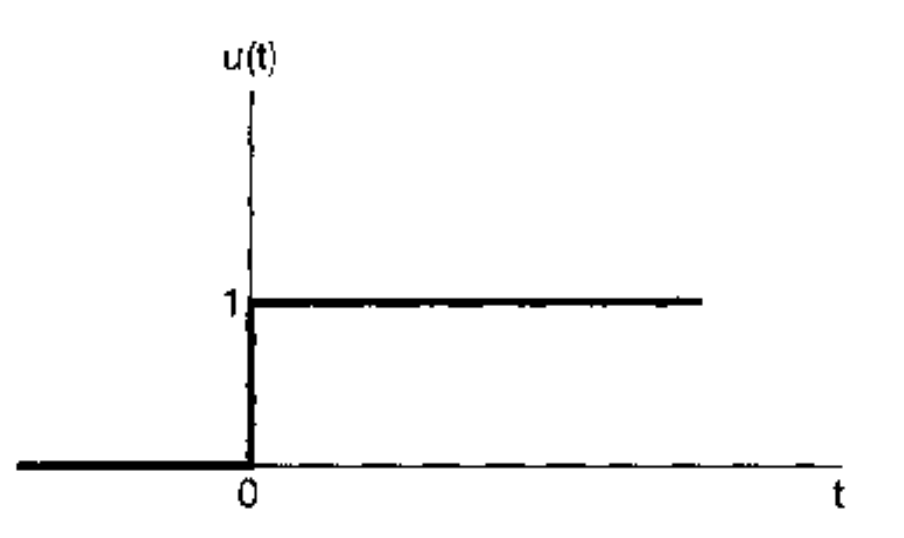
连续时间单位阶跃函数:
$$
u(t) =
\left{
\begin{aligned}
1, & t \geq 0\
0, & t < 0
\end{aligned}
\right.
$$
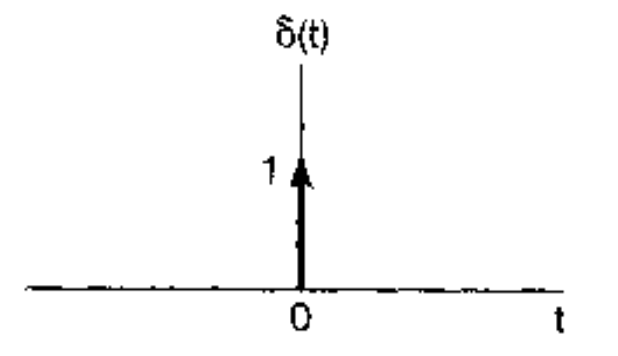
连续时间单位脉冲函数:
$$
\delta(t) =
\left{
\begin{aligned}
1, t = 0 \
0, t \neq 0
\end{aligned}
\right.
$$
关系:
$$
\delta (t) = \frac{du(t)}{dt}
$$
$$
u(t) = \int_{-\infty}^{t} \delta(\tau) d\tau
$$
卷积
对于线性时不变系统,离散时间下的卷积公式:
$$
y[n] = \sum_{k = -\infty}^{+\infty} x[k]h[n - k]
$$
记为:
$$
y[n] = x[n] * h[n]
$$
相当于把$h[n]$沿y轴翻转后向右平移n个单位,得到函数$h_1[n]$,再将$h_1[n]$与$x[n]$相乘并求线性组合,即可得到卷积结果$y[n]$
当$h[n]$为脉冲序列时,卷积相当于将$x[n]$复制到每一个脉冲的位置
连续时间下的卷积公式:
$$
y(t) = \int_{-\infty}^{+\infty} x(\tau)h(t - \tau)d\tau
$$
记为:
$$
y(t) = x(t) * h(t)
$$
卷积的性质:
交换律
分配律
结合律
傅里叶级数
傅里叶级数可以理解为复指数的线性组合
连续时间
连续时间傅里叶级数:
$$
x(t) = \sum_{-\infty}^{+\infty}a^k e^{jkw_0t}
$$
傅里叶级数系数:
$$
a_k = \frac{1}{T} \int_{T} x(t) e^{-jkw_0t} dt
$$
该系数又称为频谱系数
需要注意,傅里叶级数的求和范围是负无穷大到正无穷大,而傅里叶级数系数的积分范围是一个周期
性质:
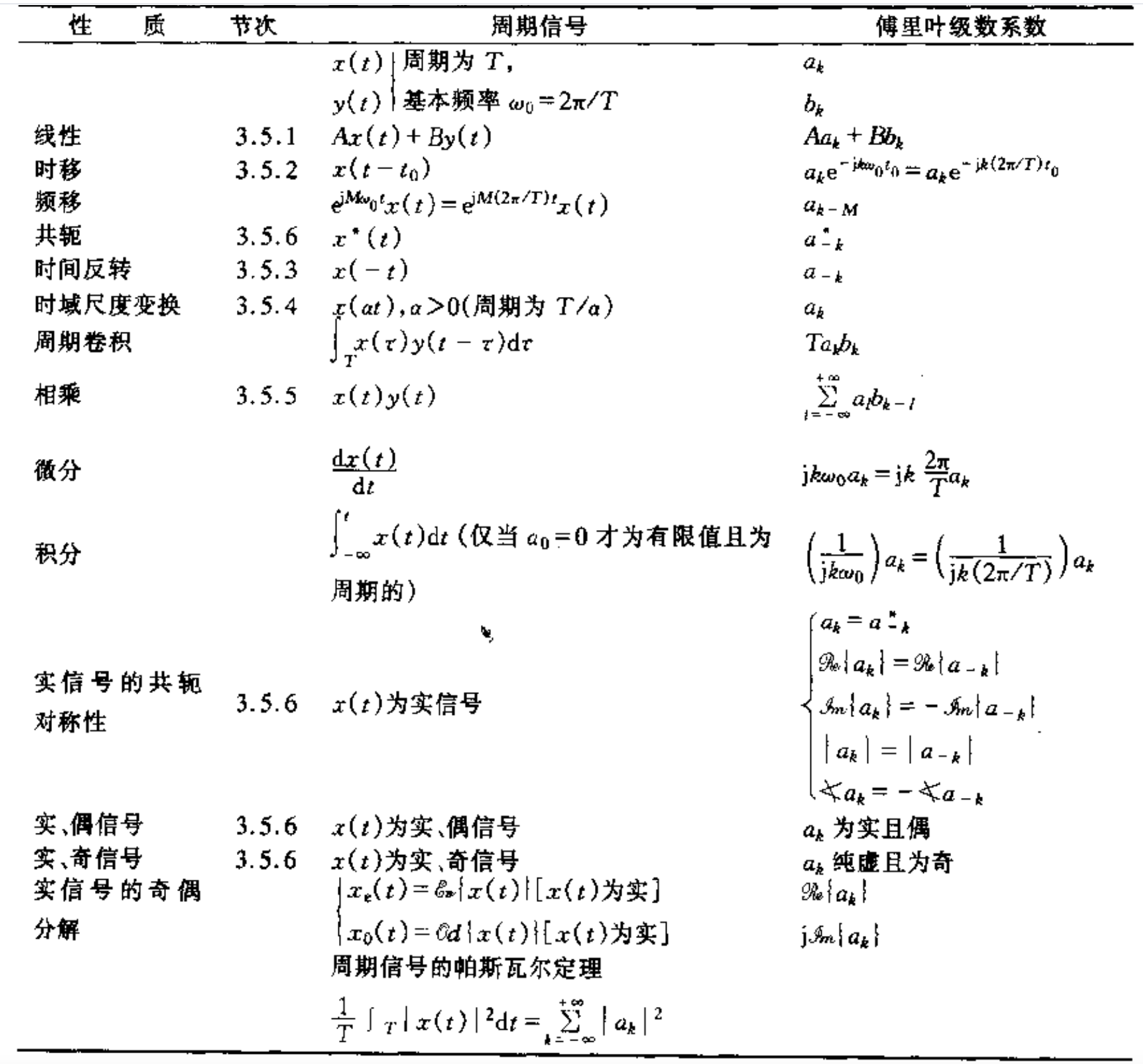
离散时间
离散时间傅里叶级数:
$$
x[n] = \sum_{k=
$$
傅里叶级数系数:
$$
a_k = \frac{1}{N} \sum_{k=
$$
离散时间傅里叶级数只对1个周期内的复指数做线性组合,这是因为$(k + N)w_0 = kw_0 + 2\pi$,即此时的复指数具有周期性
性质:

傅里叶变换
连续时间
连续时间非周期信号的傅里叶变换:
$$
x(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} X(jw)e^{jwt} dw
$$
$$
X(jw) = \int_{-\infty}^{+\infty} x(t) e^{-jwt} dt
$$
可记为:
$$
x(t) \overset{\mathscr{F}}{\longleftrightarrow} X(jw)
$$
其中,$X(jw)$是$x(t)$的傅里叶变换,它告诉我们将$x(t)$表示为不同频率正弦信号的线性组合所需要的信息,即信号的频域
这里的思想是,将信号的周期设为无穷大,则频率趋近于0,周期信号就近似地变为非周期信号。同时,组成信号的复指数成分之间的频率差异也趋近于0,$w = kw_0$可视为连续
对于周期信号而言,其傅里叶级数系数为非周期傅里叶变换的一个样本,因为此时的频率$w_0$为一固定的值,对应的$w = kw_0$是离散的点
同时,一个傅里叶级数系数为$a_k$的周期信号的傅里叶变换,可以看成是出现在谐波关系的频率上的一串冲激函数,发生于第$k$次谐波频率$w_0$的冲激函数的面积是第$k$个傅里叶级数系数$a_k$的$2\pi$倍,用公式表述为:
$$
X(jw) = \sum_{-\infty}^{+\infty} 2\pi a_k \delta(w - kw_0)
$$
连续时间傅里叶变换的性质:

利用微分和积分的性质,可以将线性常系数微分方程先进行傅里叶变换,求解后在进行逆变换,还原成方程的最终解
在时域下做卷积等价于在频域下做乘积,该性质常用于滤波,如低通滤波器、高通滤波器
在时域下做乘积等价于在频域下做卷积,相当于位移信号的频率,该性质常用于调制,如复指数调制、正弦调制,频分多路复用
连续时间基本傅里叶变换对:

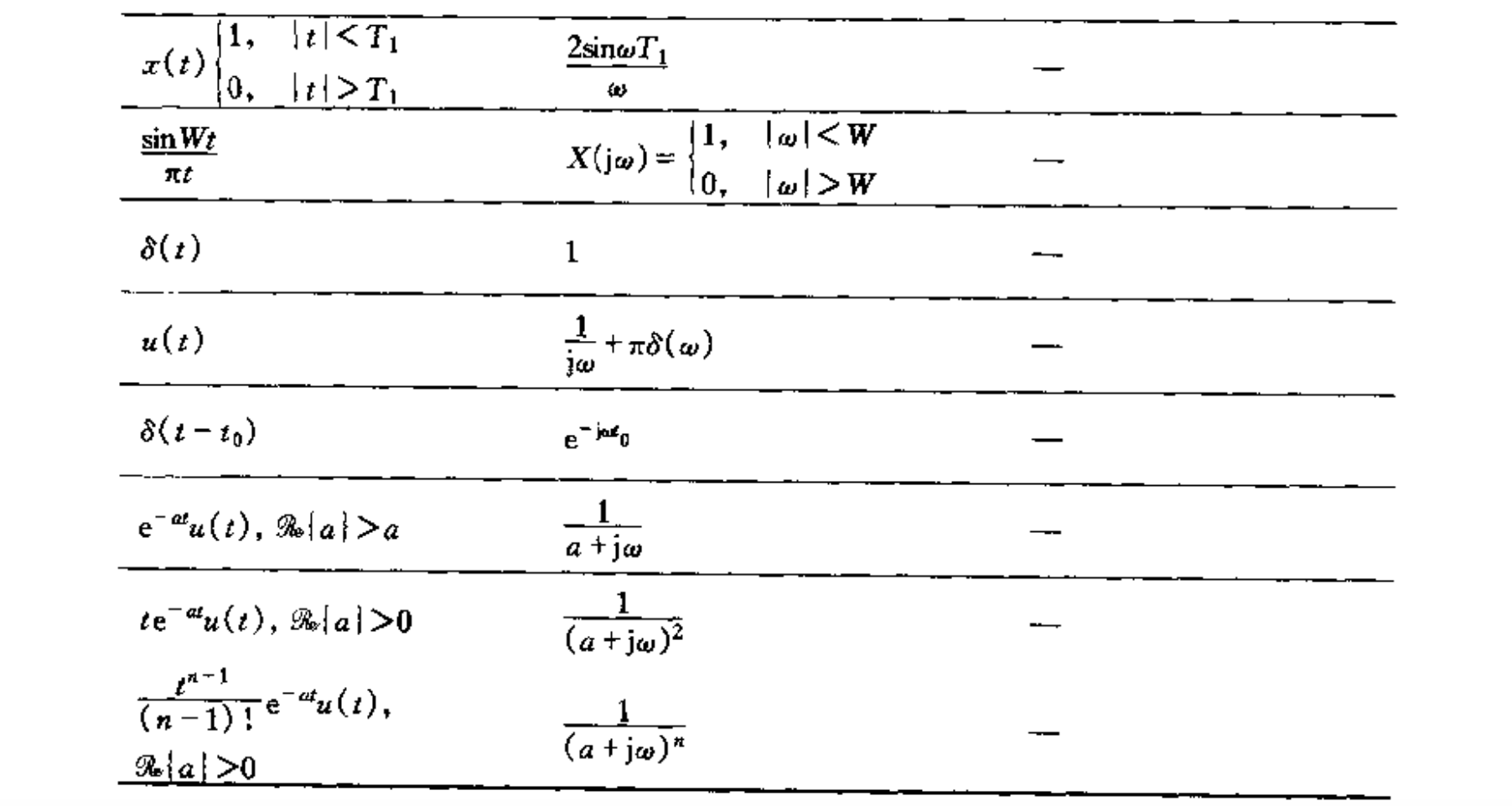
离散时间
离散时间非周期信号的傅里叶变换:
$$
x[n] = \frac{1}{2\pi} \int_{2\pi} X(e^{jw})e^{jwn}dw
$$
$$
X(e^{jw}) = \sum_{m = -\infty}^{+\infty} x[n] e^{-jwt}
$$
在离散时间下,傅里叶变换具有周期性
周期信号的傅里叶级数系数同样是非周期信号傅里叶变换的一个样本
离散时间傅里叶变换的性质:

离散时间基本傅里叶变换对:



对偶关系
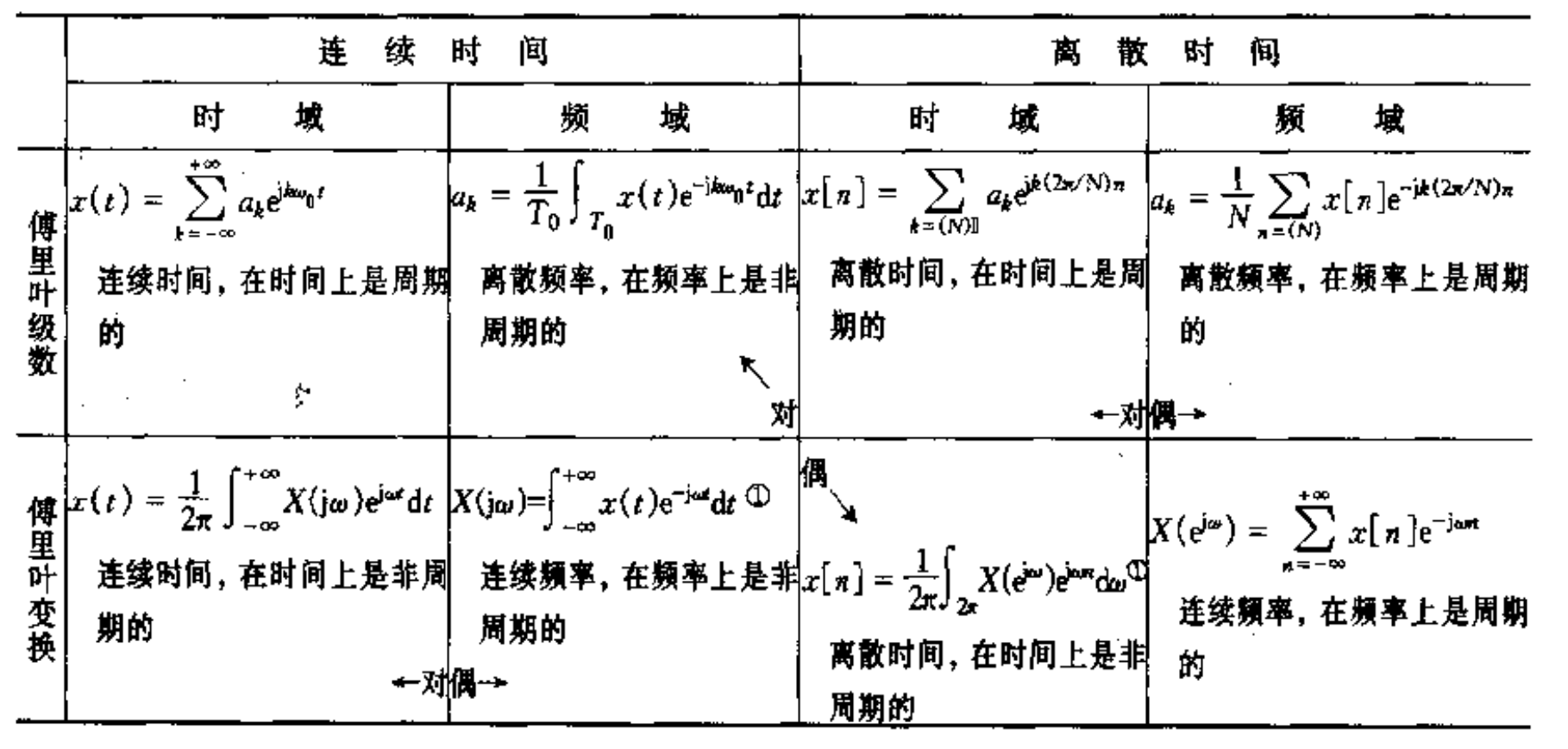
采样定理
在一定条件下,一个连续时间信号完全可以用该信号在等时间间隔点上的值或样本来表示,并且可以用这些样本值把信号全部恢复出来
采样混叠(aliasing)
如果采样频率$w$小于信号最大频率$w_m$的两倍,则会发生频率混叠,导致高频的成分变成低频。因此,只有受限带宽才可能不发生混叠
采样和重建的一般步骤:
- 使用脉冲串采样,在频域中得到周期性的频率变化
- 使用低通滤波器重建,在频域中截取频率
采样率转换:
抽取(降采样):降低采样周期,去掉中间的0值
内插(升采样):提高采样周期,在中间添加0值
离散时间采样:
$x[n]$ -> 采样 -> $x_p[n]$ -> 抽取 -> $x_d[n]$ -> 内插 -> $x_p[n]$ -> 滤波重建 -> $x[n]$