PBRT-反射模型

前置概念

表面反射模型来源

测量数据：测量得到的真实世界表面反射分布特性

现象学模型：试图描述真实世界表面定性特性的方程，往往具有修改其行为的直观参数

模拟：模拟来自微观几何的光散射以生成反射数据

物理光学：使用光的详细模型推导，计算成本往往很高

几何光学：与模拟方法一样，如果已知表面的低级散射和几何特性，有时可以直接从这些描述中导出封闭形式的反射模型

反射类别

漫反射

在所有表面上均匀散射光

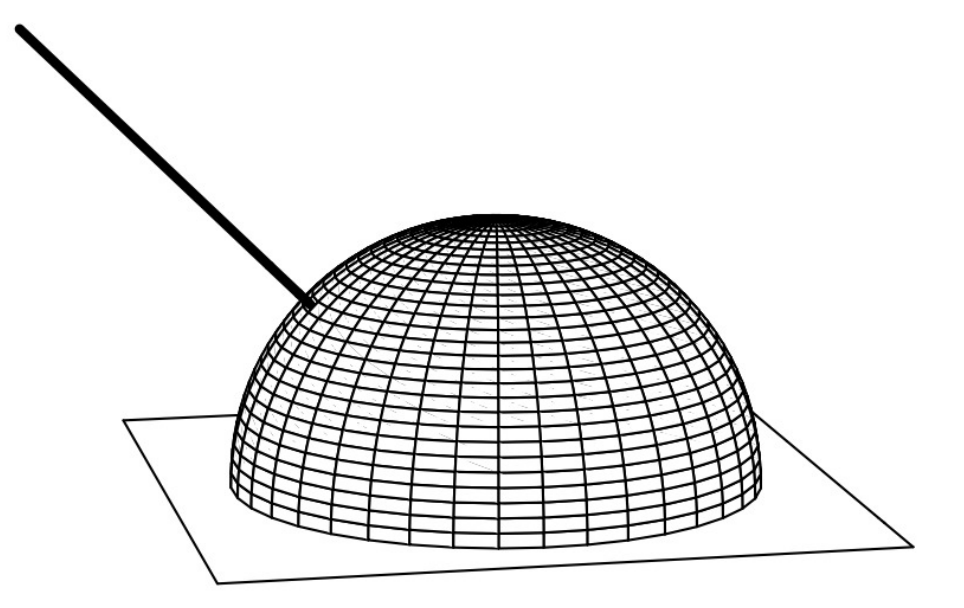
光泽镜面反射

优先在一组反射方向上散射光，它们显示其他对象的模糊反射，如塑料或高光涂料

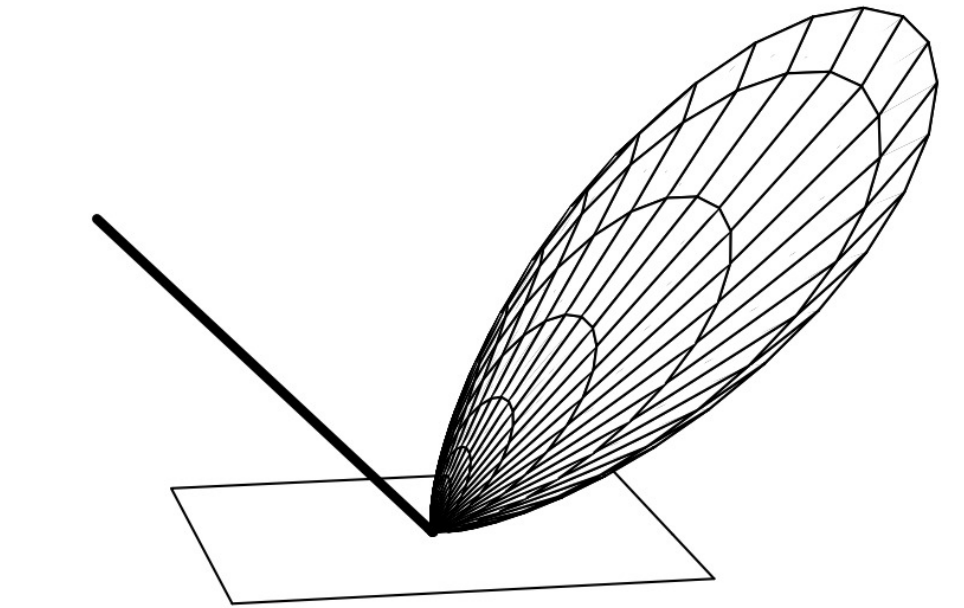
完美镜面反射

将入射光散射到一个单一的出射方向，如镜子和玻璃

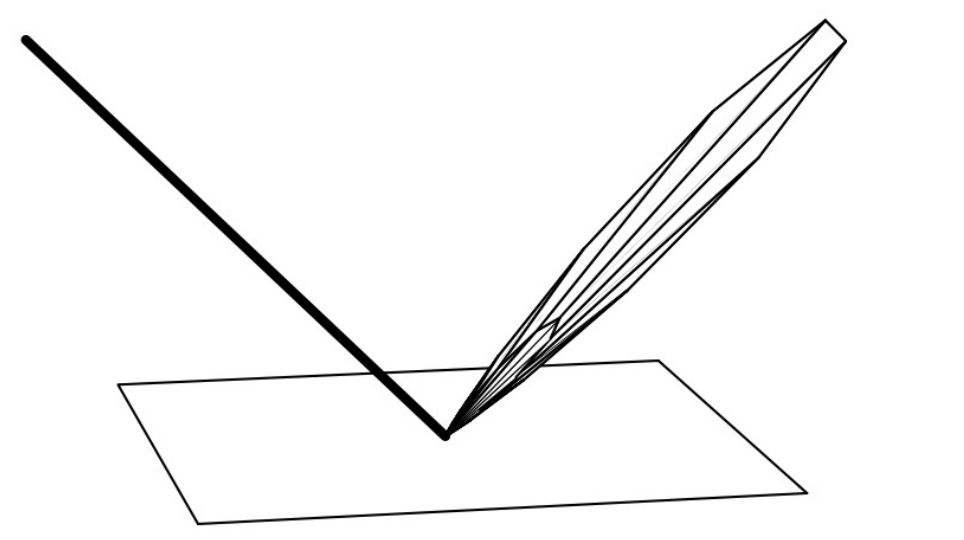
逆反射

沿着入射光的方向散射光

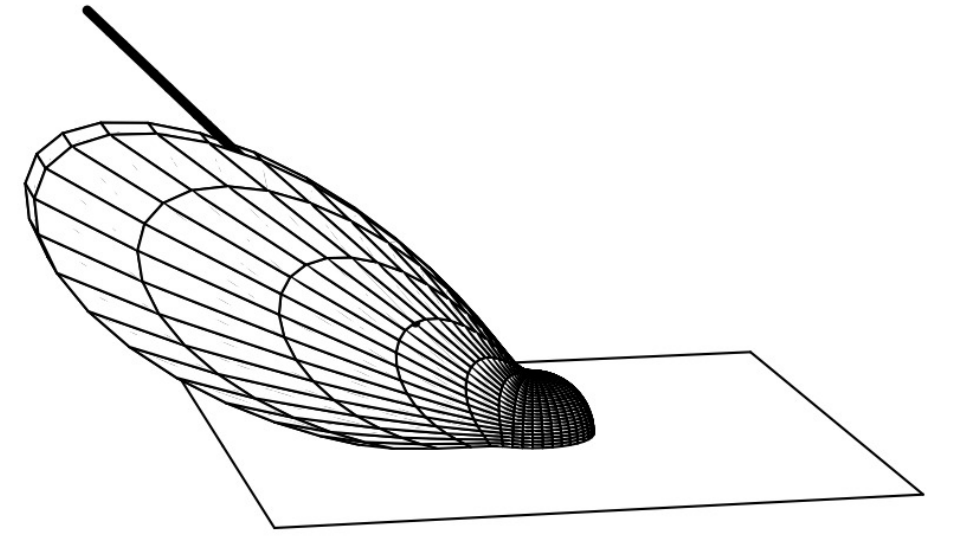
大多数反射分布函数是各向同性的，即入射光沿绕着一个点的法线轴进行旋转，其反射光的分布不会改变。对于各向异性而言，则会反射不同数量的光，比如拉丝金属、布和光盘

材质类别

• 电介质，是不导电的材质。它们具有实数值的折射率并透射一部分入射光，如玻璃、矿物油、水、空气
• 金属导体。材质是不透明的，并反射大部分照明，一部分光也传输到导体内部被吸收，在pbrt中忽略透射效应，只对导体的反射分量进行建模，导体具有复数值的折射率$\bar\eta = \eta + i k$
• 半导体。pbrt中不讨论这种材质

反射坐标系

计算反射时使用的坐标系，由正交基向量$(s, t, n)$定义，在调用BSDF方法之前，世界空间中的$w$方向向量被转换到该坐标系中

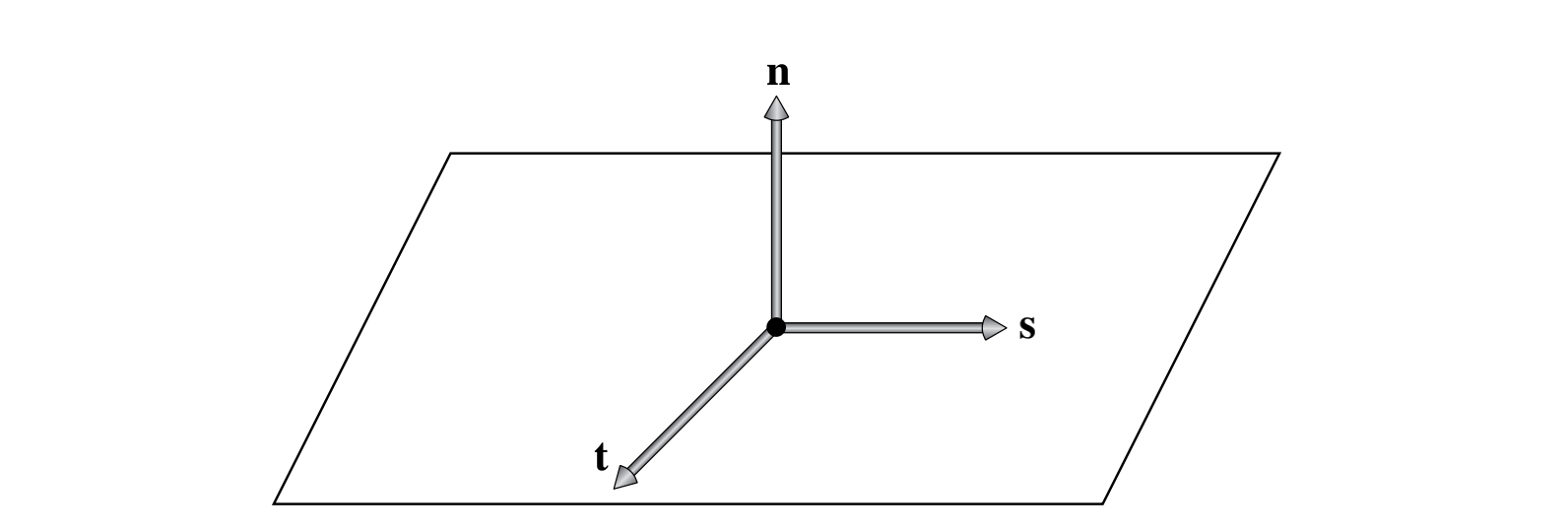
也可以使用球坐标来表示：

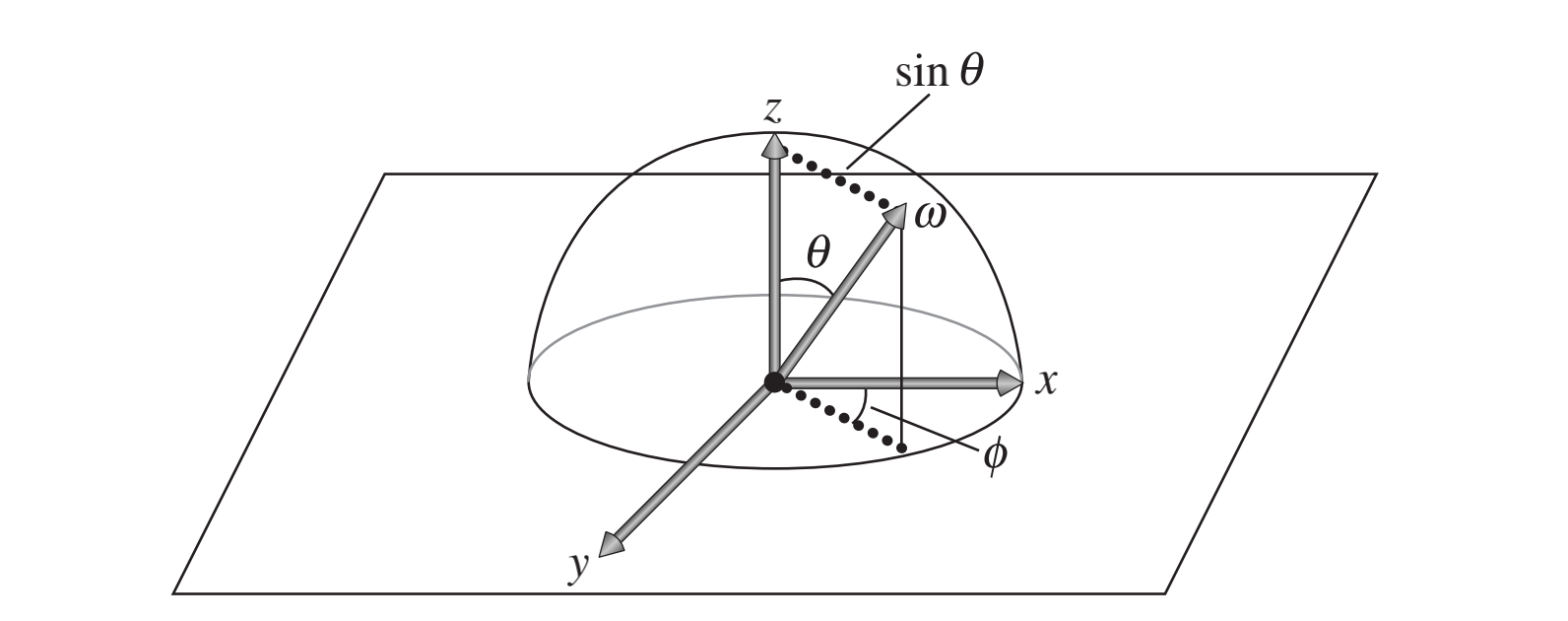
其转换公式为：

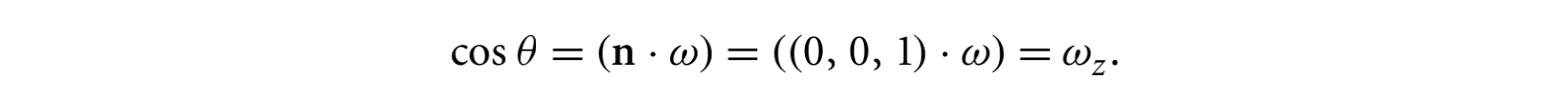
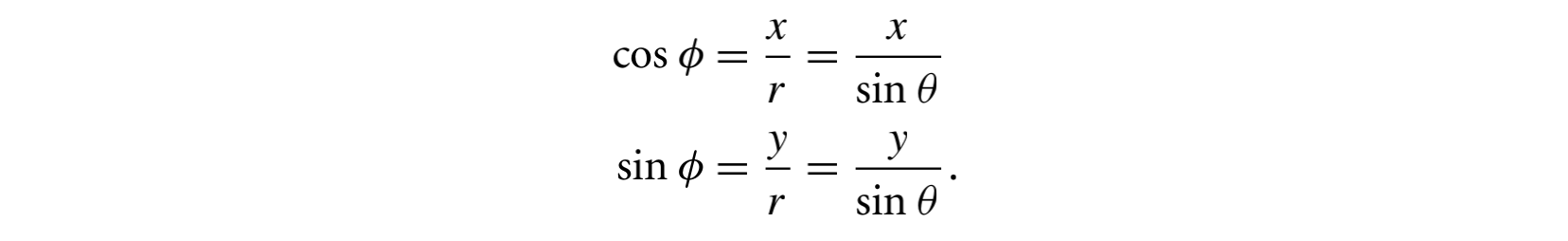
反射率

半球-方向反射率是一个2D函数，它在给定方向上由于在半球上的恒定照明而产生全反射，或者等效地，由于来自给定方向的光而在半球上产生全反射，他被定义为

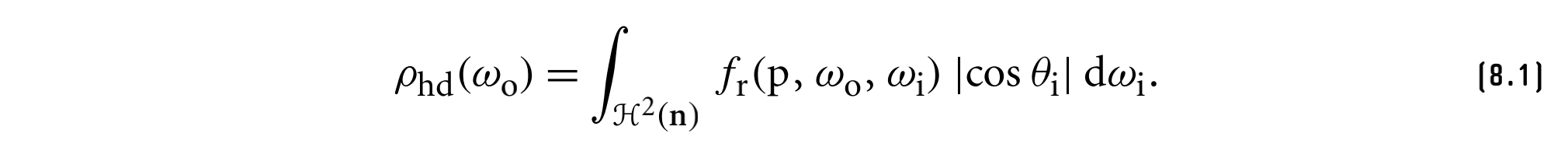
注意，该方程和散射方程相比少了入射辐射度那一项，即$L_i(p, w_i)$

表面的半球-半球反射率公式如下：

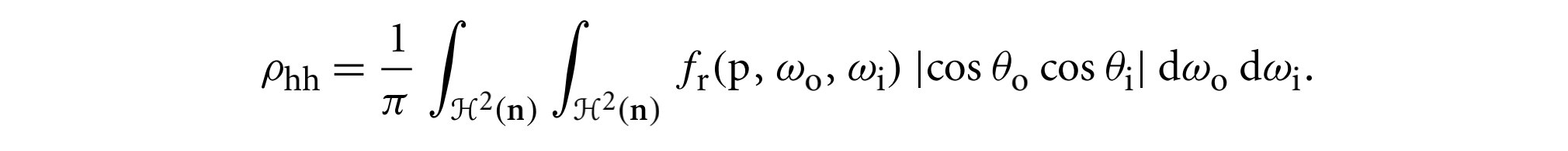
当入射光的方向相同时，它给出表面反射的入射光的分量。对于内层积分，得到的是给定入射方向下整个半球上的反射率，对于外层积分，得到的是所有入射方向得到的半球反射率的总和

镜面反射和透射

出射方向和入射方向两者相对发现的夹角相同
$$
\theta_i = \theta_o
$$
其中$\phi_o = \phi_i + \pi$，对于透射而言，也有相同的$\phi$方程，输出方向$\theta_t$由斯涅尔(Snell)定律给出，折射率描述了光在特定介质中的传播速度比在真空中慢多少，Snell定律如下：

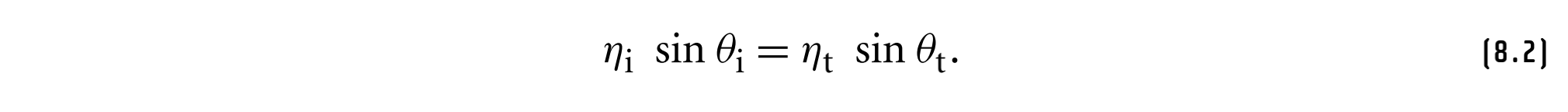
一般来说，折射率随着光的波长而变化，入射光通常在两种不同介质之间的边界处向多个方向散射，这种效应称为色散。在图形学中往往忽略这种波长相关性

菲涅耳反射(Fresnel Reflection)

Snell定律给出了透射方向的计算方法，此时还需要计算被反射或透射的入射光比例

给定折射率和入射光线与表面法线的夹角，菲涅耳方程指定了材质对入射照明的两种不同偏振态的相应反射比，pbrt中假设光是非偏振的，则反射比是平行和垂直偏振项的平方的平均值(注：这里的定义和维基百科中不同，后者定义为算数平均值)

维基百科的解释：https://zh.wikipedia.org/zh-cn/%E8%8F%B2%E6%B6%85%E8%80%B3%E6%96%B9%E7%A8%8B

注意区分折射率和透射比的区别

折射率表，给出真空中光速与介质中光速之比

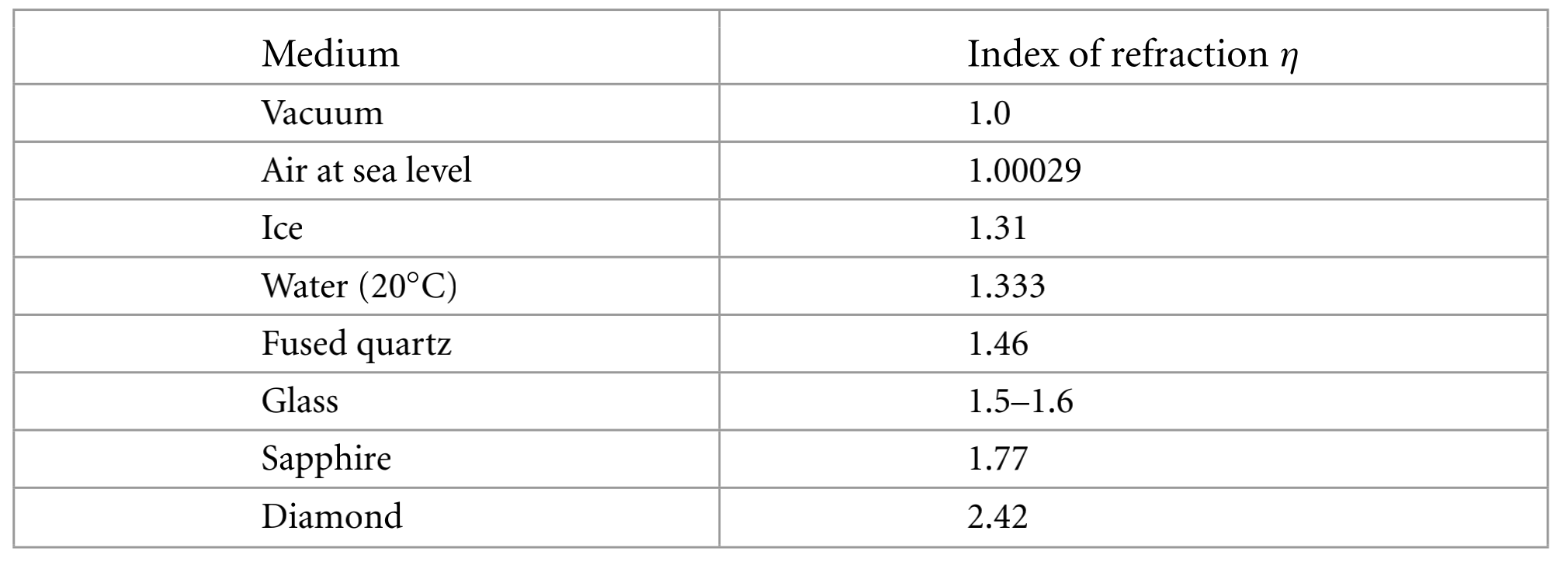
电介质的菲涅耳反射比公式为

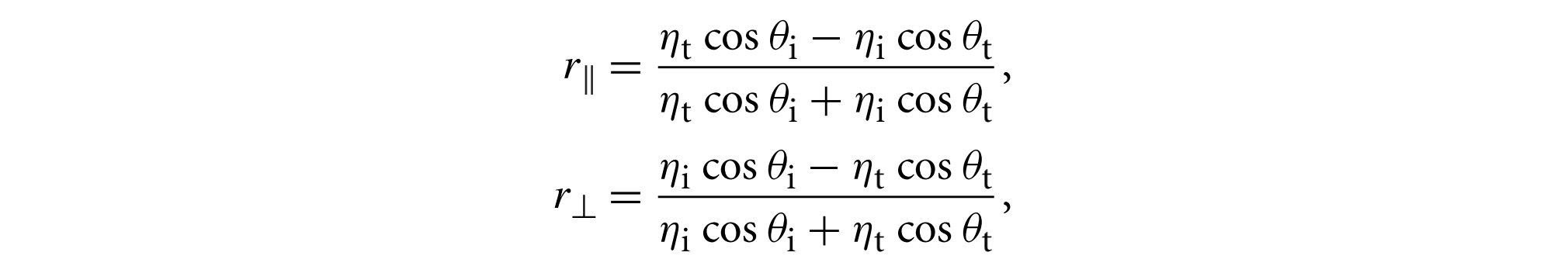
两者分别为平行偏振光的反射比和垂直偏振光的反射比。余弦项应该全部大于或等于0，因此计算$cos\theta_i$和$cos\theta_t$时，几何法线应该分别翻转到与$w_i$和$w_t$的同一侧

对于非偏振光，菲涅耳反射比为

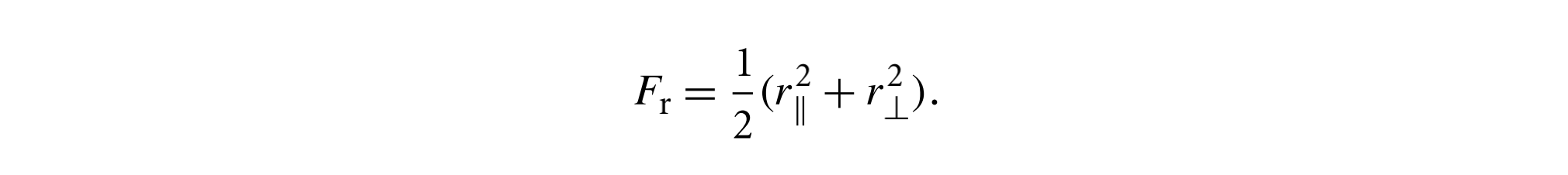
透射比为$1 - F_r$

对于复折射率$\bar\eta = \eta + i k$而言，其中一些入射光可能被材质吸收并转化为热量。其中$k$是吸收系数

导体和电介质之间边界处的菲涅耳反射比由如下公式给出：

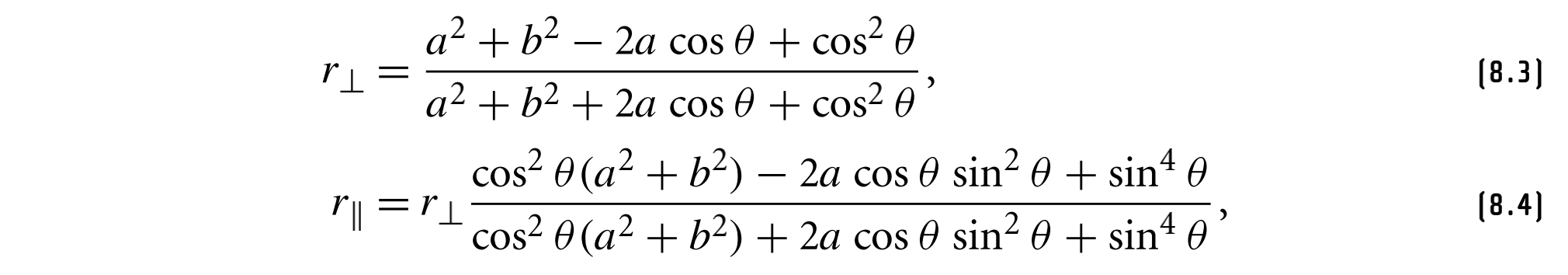
其中

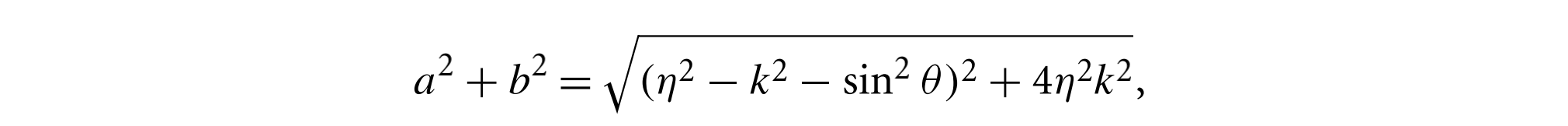
镜面反射

菲涅耳方程给出了反射光的分量，$F_r(w)$，我们需要一个BRDF使得

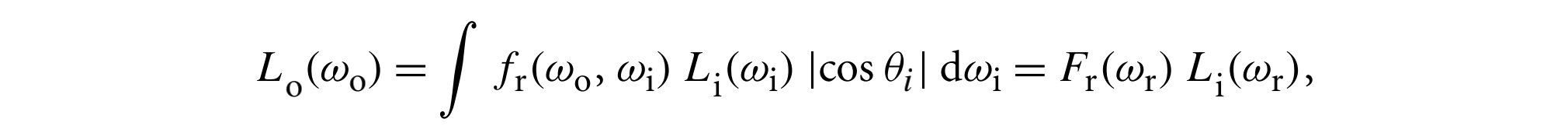
其中$w_r = R(w_0, n)$是$w_0$关于表面法线$n$反射的镜面反射向量

由于镜面反射时，一个入射方向只会对应一个出射方向，因此使用冲激函数来表达BRDF，代换相关因子得

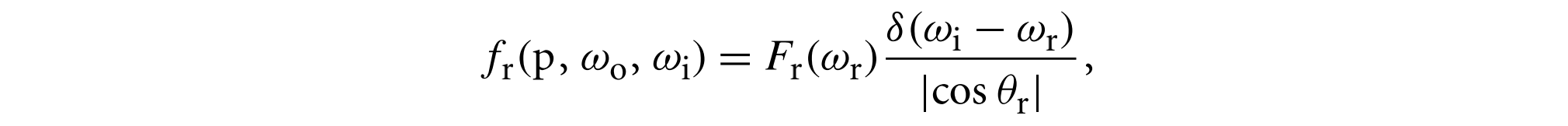
反射向量$w_r$的计算方法为

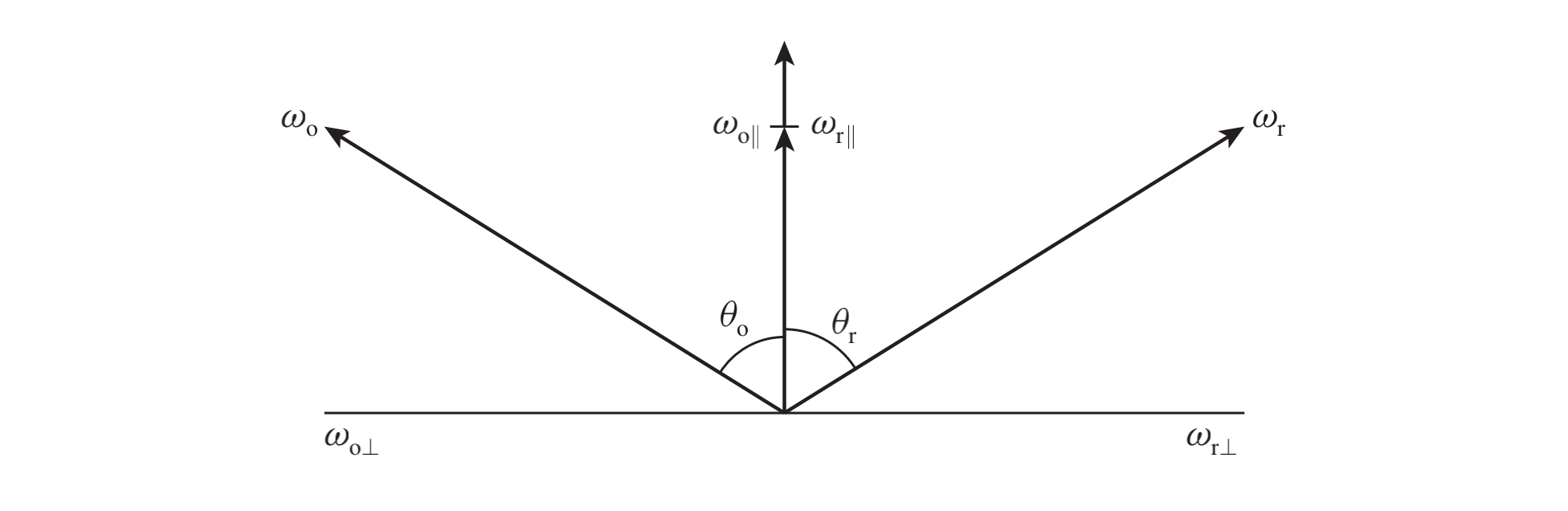
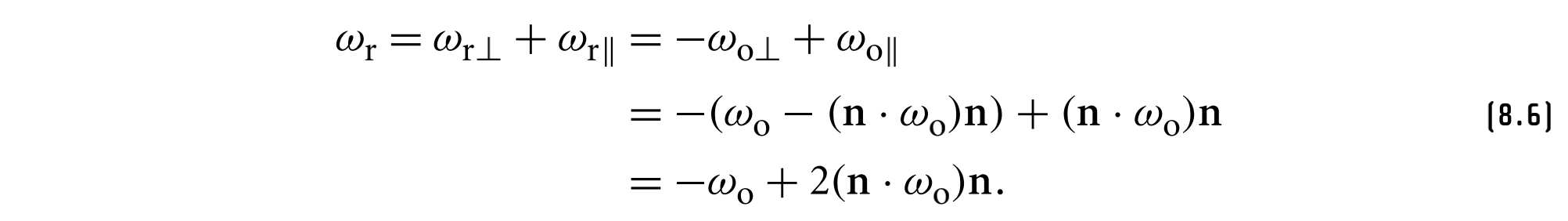
镜面透射

使用$\tau$表示由菲涅耳方程给出的透射到出射方向的入射能量的分量，因此$\tau = 1 - F_r(w_i)$，则透射的通量微分为

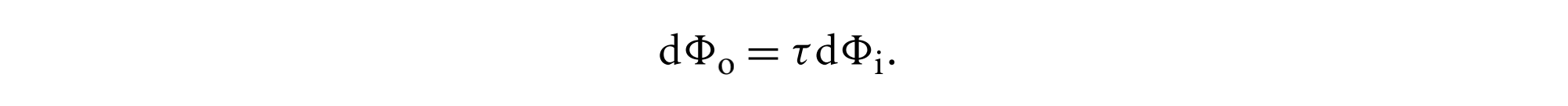
根据定义有

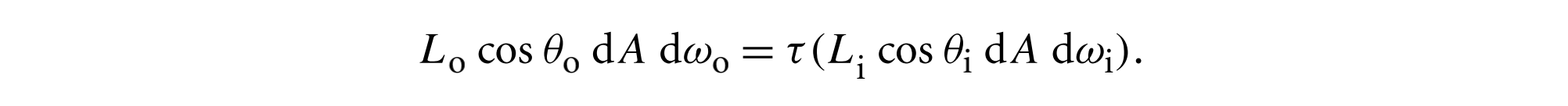
将立体角转化为球面角

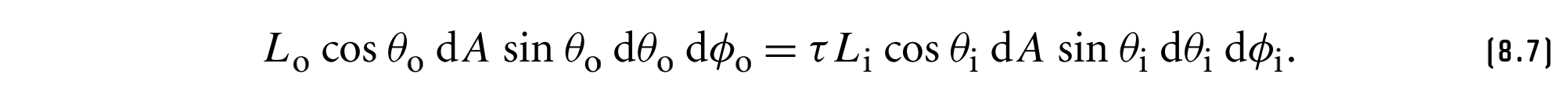
对斯涅尔定律关于$\theta$微分，则有

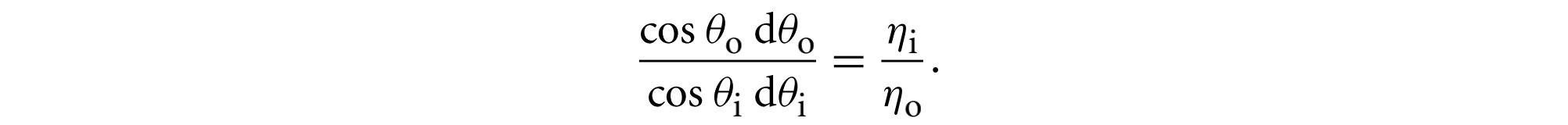
综合上述2个方程有

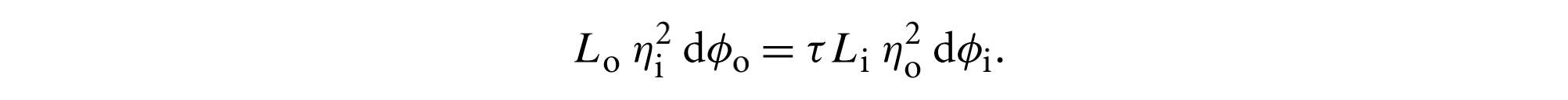
因为$\phi_i = \phi_o + \pi $，因此$d\phi_i = d\phi_o$，最终有出射辐射度关于入射辐射度、折射率、透射比的关系

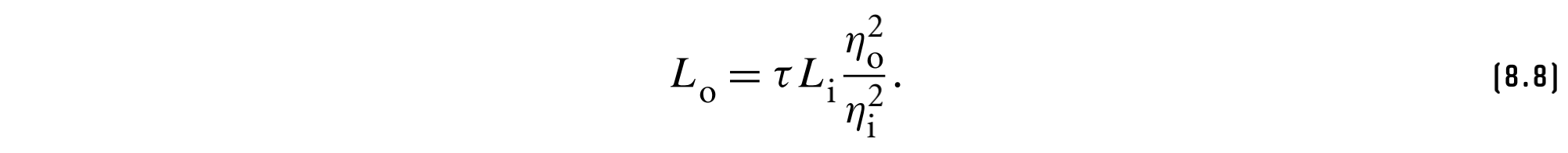
类似地，根据散射方程以及上式得到BTDF函数的表达式如下

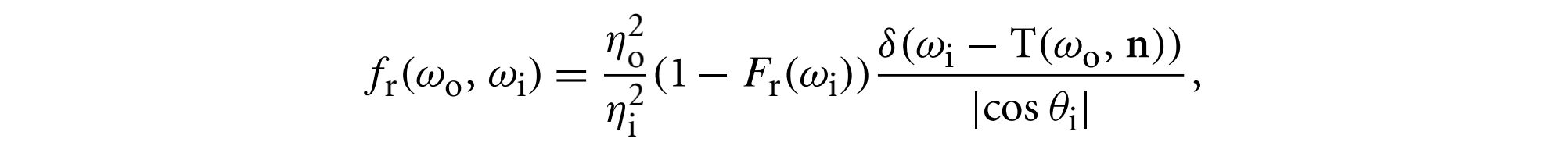
其中$T(w_o, n)$是镜面透射向量

透射方向$w_t$的计算方法为

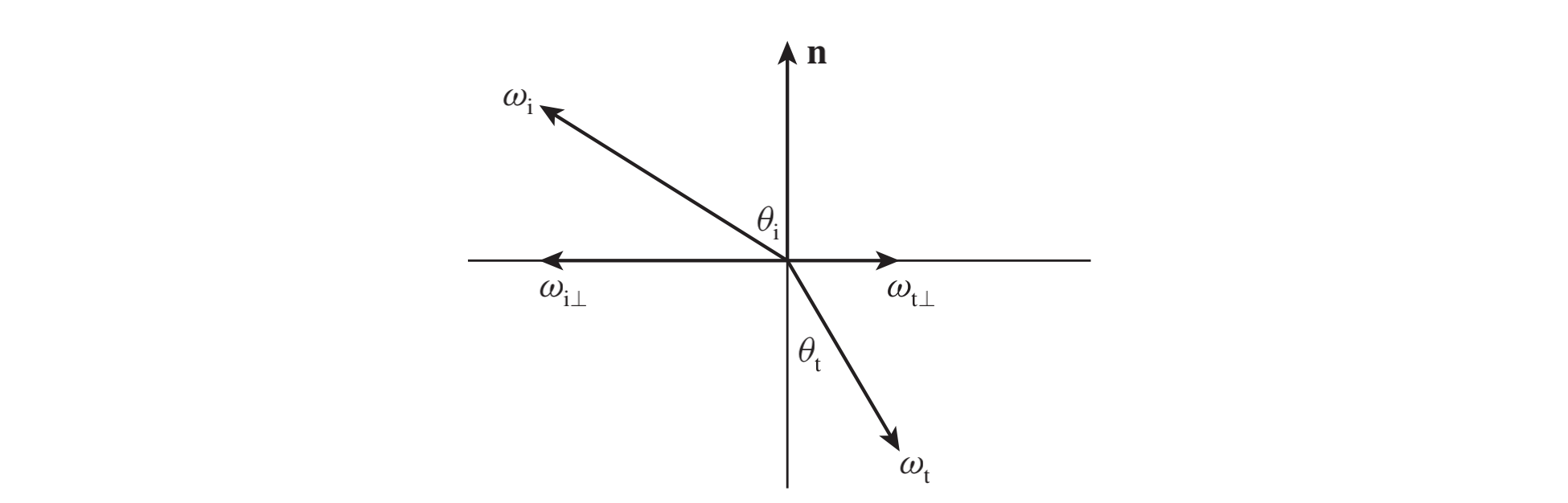
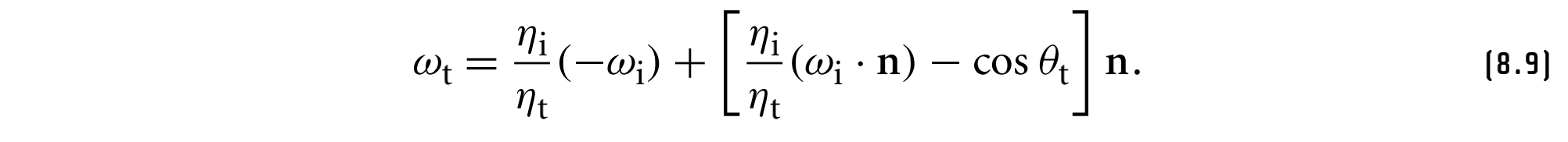
其中，$w_i, w_o, n$都是单位向量，$n$朝向入射介质的一边

$cos\theta_t$的计算公式为

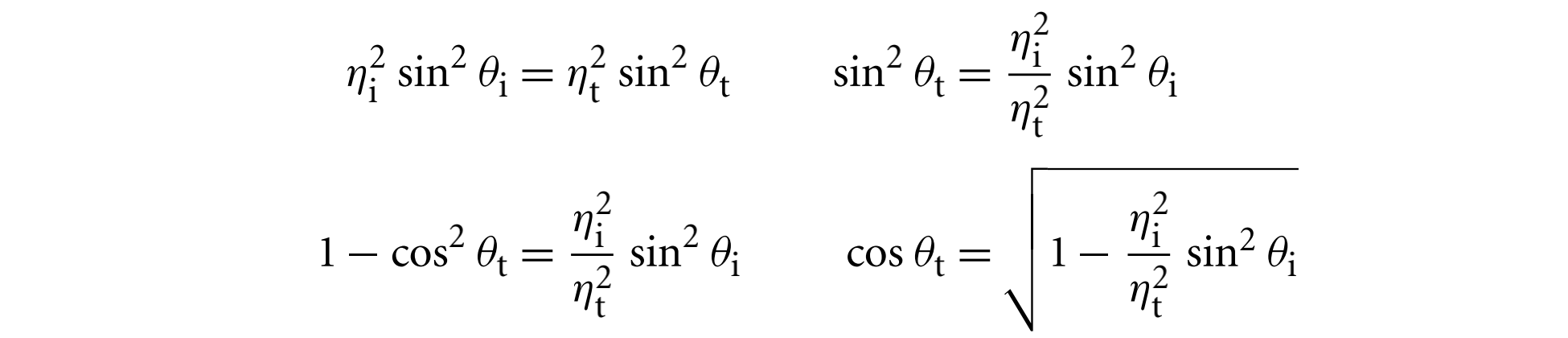
兰伯特反射(Lambertian Reflection)

Lambertian模型模拟了一个完美的漫反射表面，该表面在所有方向上均等地散射入射照明，其反射分布函数为$f = R/\pi$，其中$R$为散射的入射光的分量

微表面模型

许多基于几何光学的表面反射和透射建模都基于这样的方法，即粗糙表面可以建模为小的微表面的集合，由微表面组成的表面通常称为高度场，其在统计上描述平面方向的分布。在pbrt中，使用microsurface描述微表面，macrosurface来描述底层的平滑表面

两种不同的微表面横截面如下

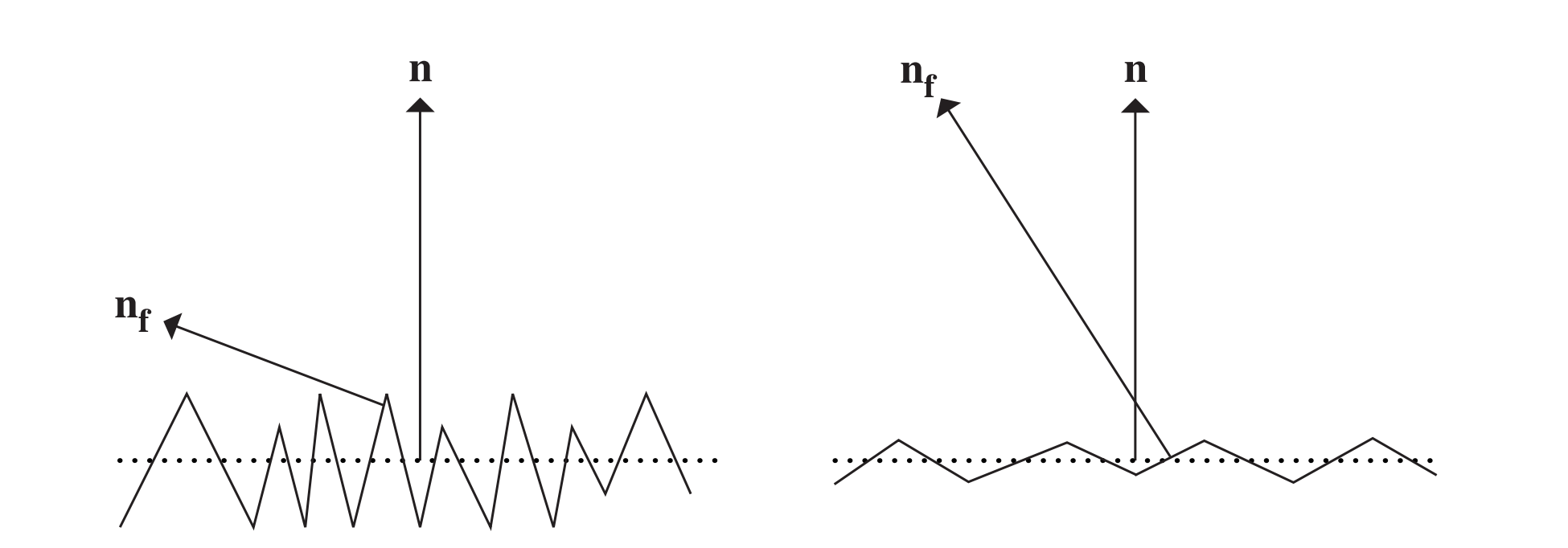
基于微表面的BRDF模型通过对来自大量微表面的光散射进行统计建模来工作，假设被照亮的微分区域$dA$与单个微表面的面积相比大很多，则此时有大量的微表面将被照亮，并且它们的聚合行为决定了观察到的散射

微表面模型的两个主要组成成分：

• 微表面的分布
• 描述光如何从单个微表面散射的BRDF

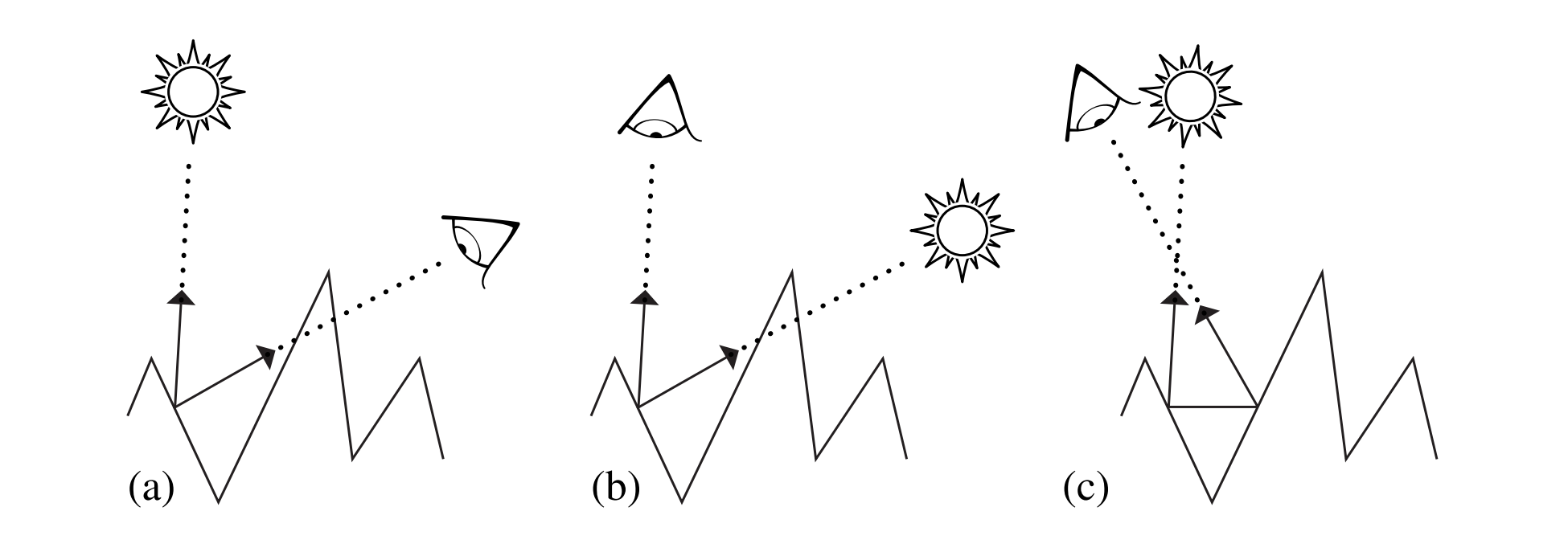
考虑微表面的局部照明效果，主要是三种情况：

• 微表面被另一个面阻挡
• 位于相邻微表面的阴影中
• 相互反射，导致微表面反射的光比直接光照和低级微表面BRDF预测的更多，因为有来自其他方向的光，见图c

Oren-Nayar漫反射

Oren和Nayer发现粗糙表面通常随着照明方向接近观察方向而显得更亮，他们提出的反射模型通过V型微表面描述粗糙表面，该微表面由球形高斯分布描述，具有单个参数$\sigma$，即微表面方向角的标准差

在V形假设下，可以通过仅考虑相邻的微表面来解释相互反射，因此，该模型推导出的BRDF对凹槽集合的聚合反射进行建模，结果考虑了微表面之间的阴影、遮蔽和相互反射，其近似公式为

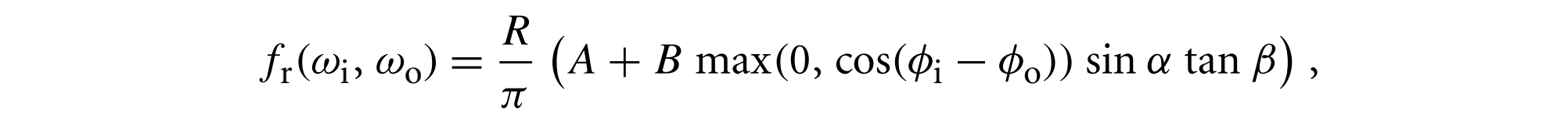
其中$\sigma$用弧度来表示，且有

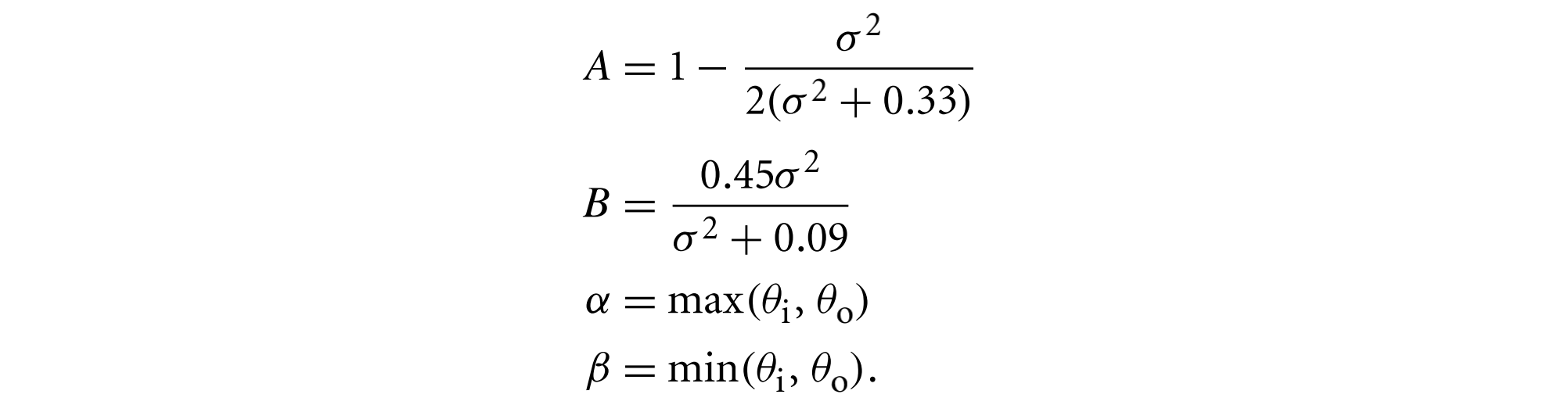
微表面分布函数

微表面的一个重要特征使用分布函数$D(w_h)$表示，它给出了具有微表面法线$w_h$的微表面的微分面积

微表面分布函数必须归一化以确保他们在物理上是合理的，如果我们考虑沿法线方向$n$在微表面上的入射光线，那么每条光线必须恰好与微表面相交一次。给定微表面的微分面积$dA$，那么该区域上方的微表面的投影面积必须等于$dA$

注：这里暂时理解为，微表面上不能出现倒下的三角形，这种情况下一条光线可能与多个微表面相交，投影面积也会有重叠

可以用公式表述为

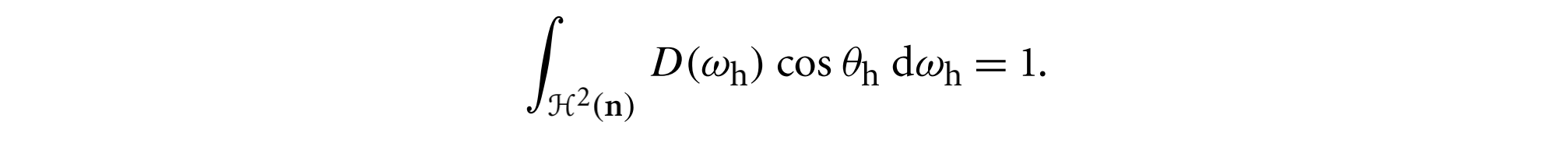
Beckmann和Spizzichino提出了一种广泛使用的基于微表面斜率高斯分布的微表面分布函数，它的传统定义是

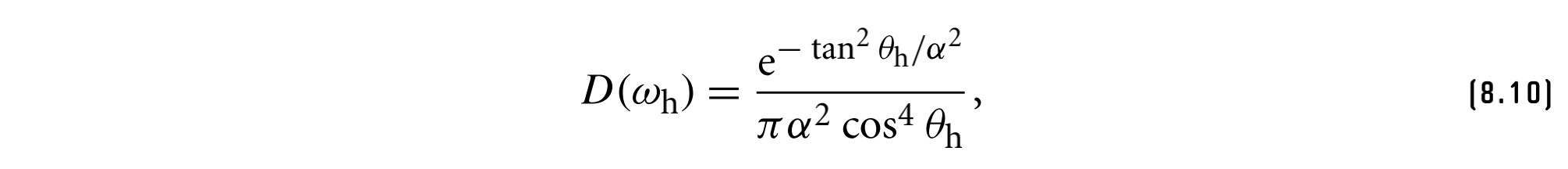
如果$\sigma$是微表面的均方根(RMS)斜率，则$\alpha = \sqrt2 \sigma$

如果是各向异性分布，其中的法线分布会随$w_h$的方位角方向而变化，例如，给定垂直于$x$轴的微表面的$\alpha_x$和$y$轴的$\alpha_y$，则中间方向的$\alpha$值可以通过这些值构造一个椭圆，相应的各向异性微表面分布函数为

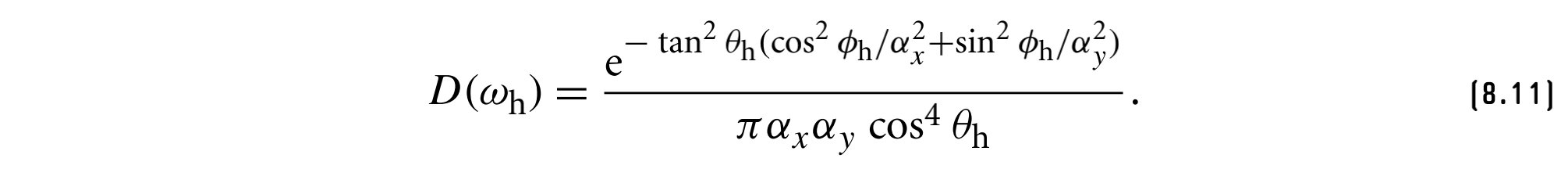
另一个有用的微表面分布函数来自Trowbridge和Reitz，其各向异性表达式由下式给出

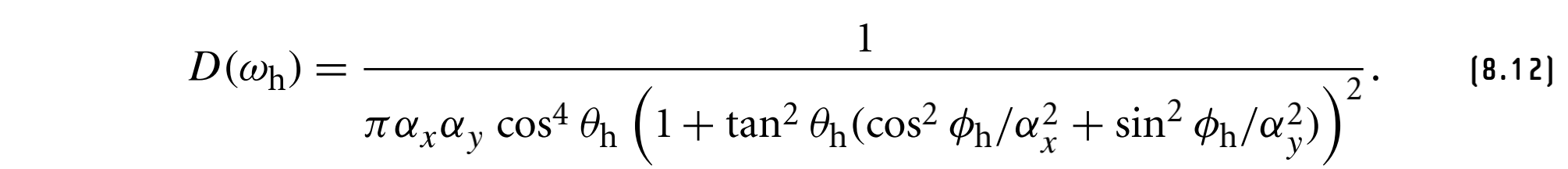
两者的函数图像如下，其中，横坐标为$\theta$的值，它是微表面法线$w_h$和宏表面法线$(0, 0, 1)$之间的夹角

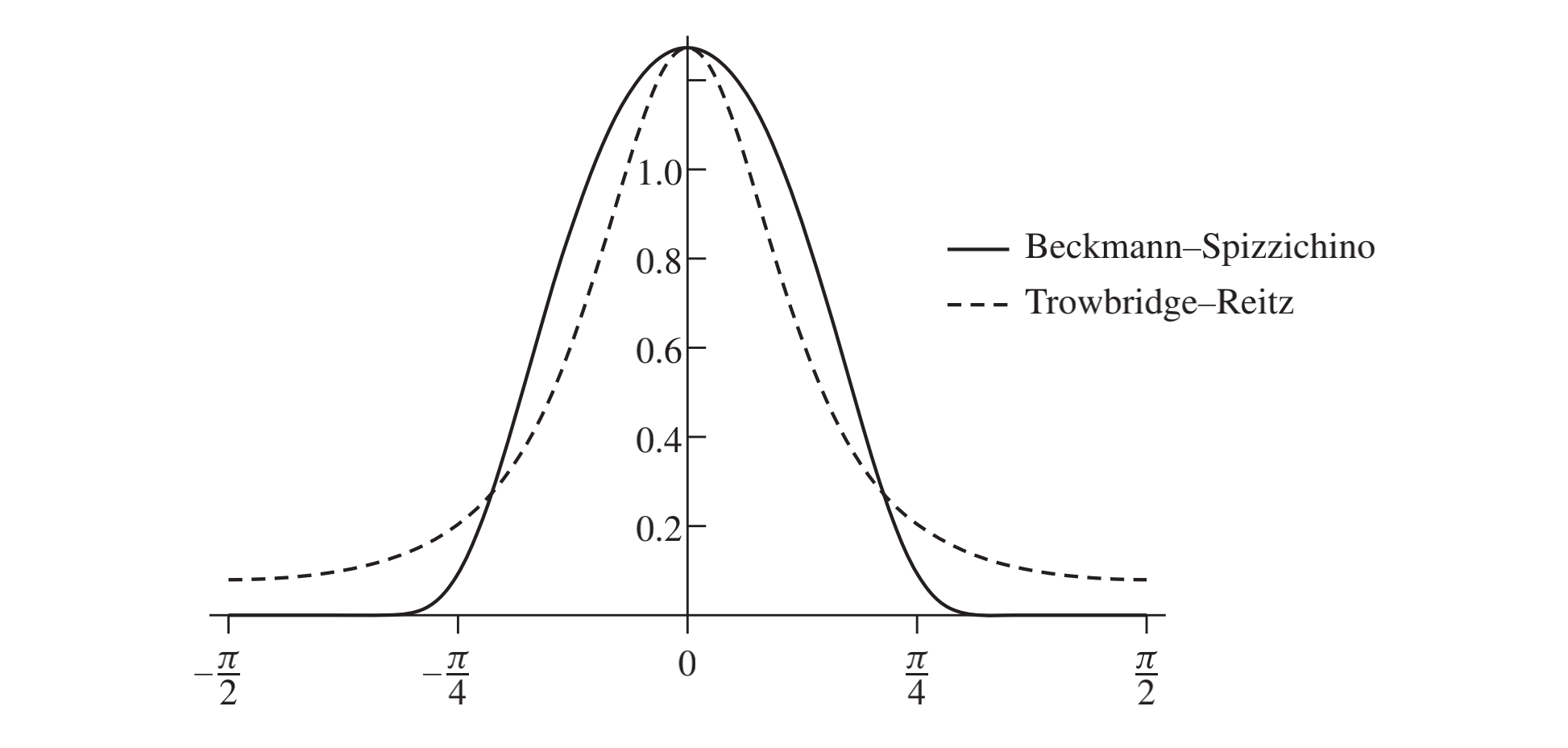
从图中可以看出，TR模型具有更高的尾部，对于远离表面法线的方向，它更慢地下降到0，该特性与许多真实世界表面非常匹配

微表面模型可以这样理解，每个平面包含多个微平面，这些微平面的取向是各种各样的，但大致满足上述函数图像的分布，即和原始取向相似的微表面法线数目更多，不相似的更少。当表面完全光滑时，所有微表面取向一致，此时就是完美的镜面反射

遮蔽和阴影

现在考虑微表面的局部照明效果，使用遮蔽-阴影函数$G_1(w, w_h)$进行建模，它给出了具有法线$w_h$的微表面从$w$方向可见的分量(或比例)。通常情况下，微表面可见的概率与其方向$w_h$无关，因此可以写成$G_1(w)$

从$w$方向看到的微表面面积为$dAcos\theta$，则$G_1$的归一化约束为

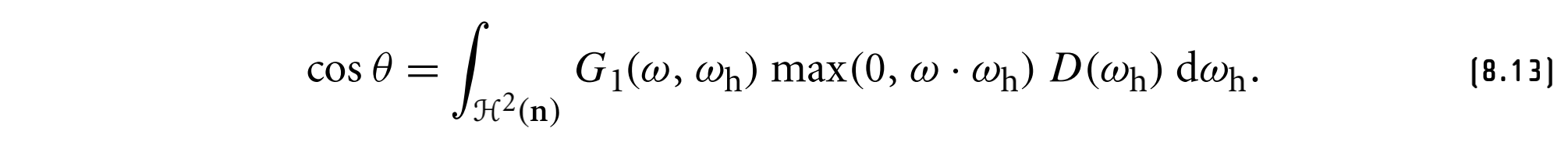
换句话说，给定方向$w$的可见微表面的投影面积必须等于$(w \cdot n) = cos\theta$乘以宏观表面的微分面积$dA$

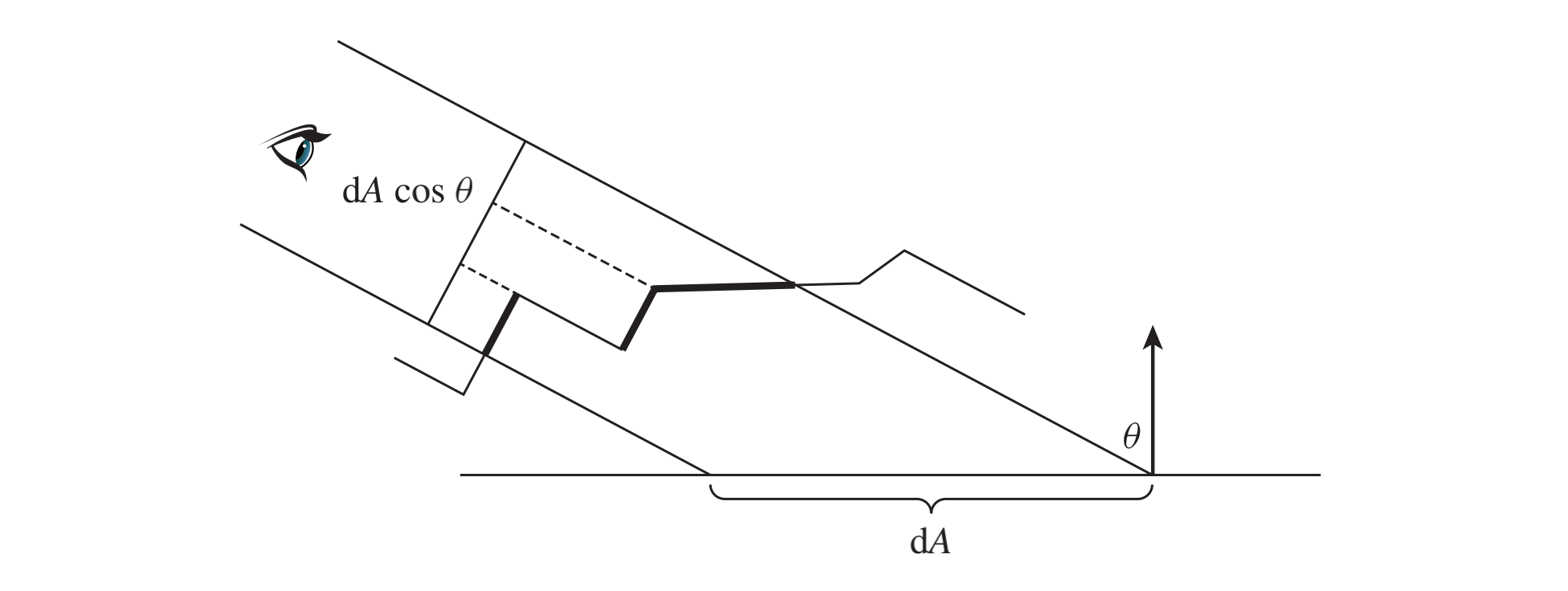
如果$A^+(w)$是从$w$方向看到的前向微表面的投影面积，而$A^-(w)$是来自方程[8.13]的后向微表面的投影面积，则$cos\theta = A^+(w) - A^-(w)$，因此，我们可以将遮蔽阴影函数写为可见微表面面积与总前向微表面面积的比率：

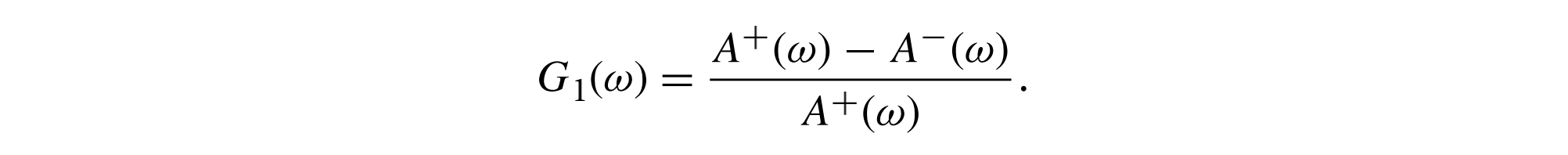
使用辅助函数$\Lambda (w)$表示每个可见微表面区域中，不可见遮蔽微表面面积：

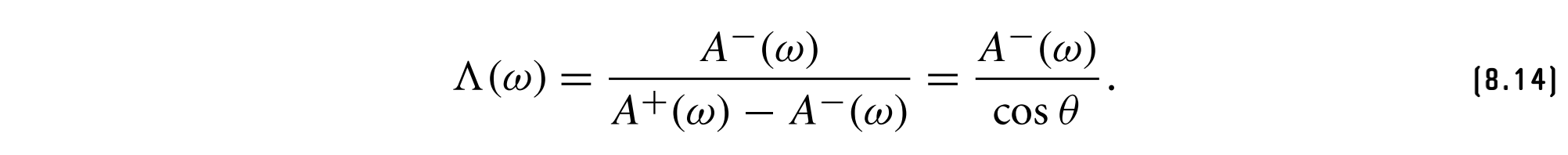
则遮蔽函数可以重新表述为

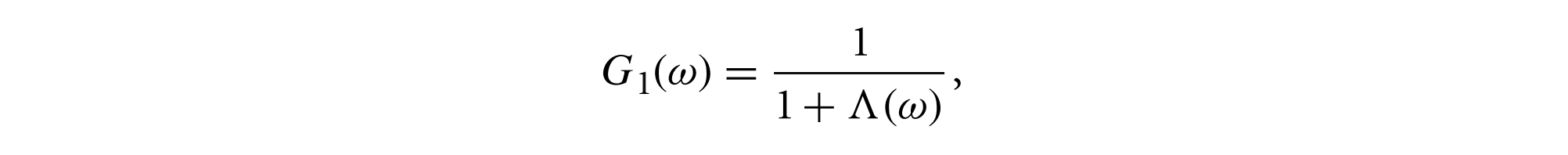
在附近点高度不相关的假设下，各向同性BeckmannSpizzichino分布的$\Lambda(w)$为

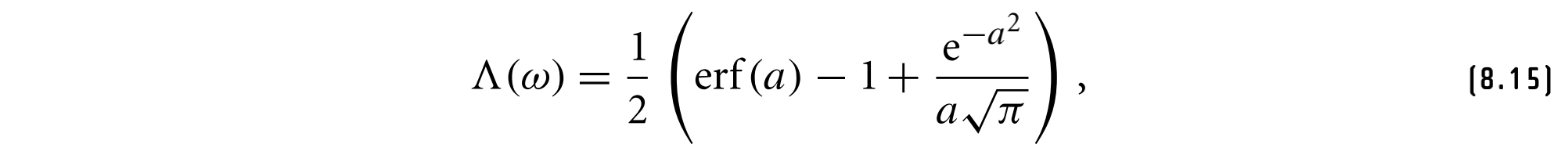
其中$a = 1/(\alpha tan\theta)$和$erf$是误差函数，$erf(x) = 2/\sqrt\pi \int_0^x e^{-{x^{‘}}^2} d x^{‘} $

在不相关高度假设下，Trowbridge-Reitz分布的$\Lambda(w)$为

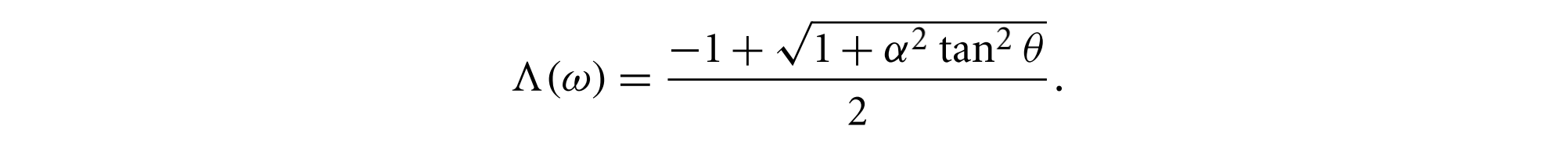
其$G_1(w)$函数图像如下

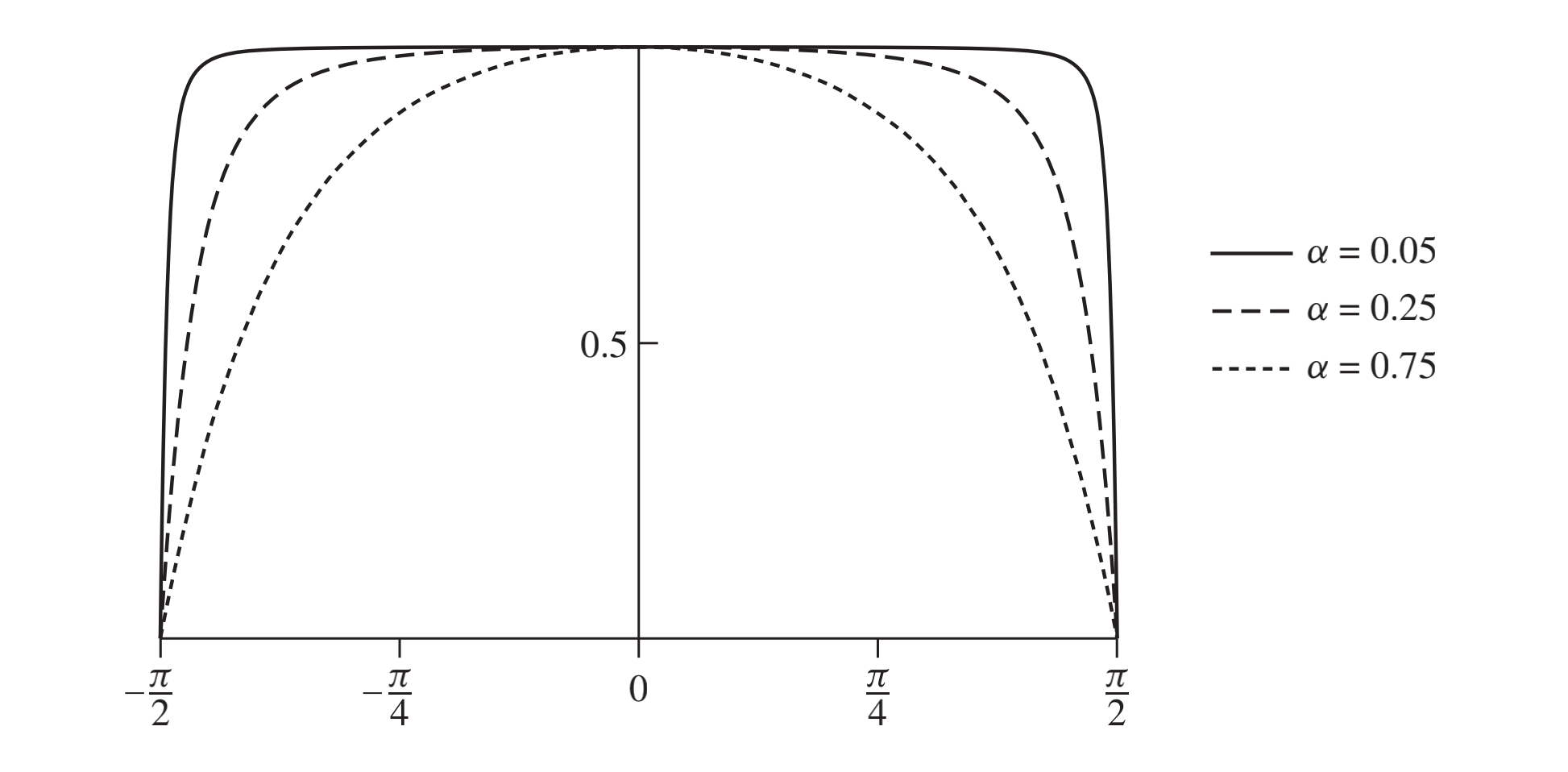
可以发现，增加表面的粗糙度会导致函数更快地下降到0，此时可见微表面更少，在视角垂直于微表面时，几乎所有微表面都不可见

与微表面分布的几何特性相关的最后一个函数是$G(w_o, w_i)$，它给出了微分区域中从$w_o$和$w_i$方向都可以看到的微表面的比例。假设一个微表面从两个方向都可见的概率，等于它从每个方向独立可见的概率之积，则有

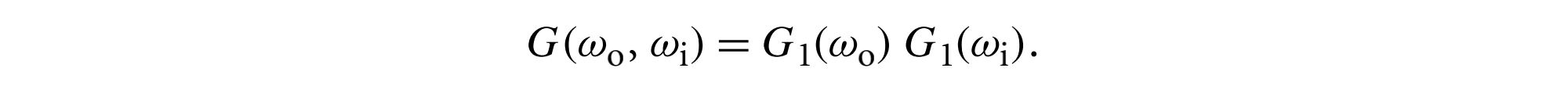
实际中两者往往并不独立，这导致$G$被低估，另一个更准确的模型认为，微表面上的给定点越靠上，微表面的可见性就越高，该模型表述为

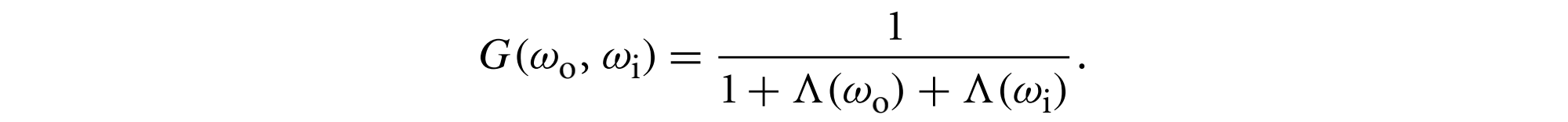
Torrance-Sparrow模型

该微表面模型用于模拟金属表面，他们将表面建模为完美光滑的镜面微表面的集合，只有那些法线等于半角向量的微表面能导致完美镜面反射，即

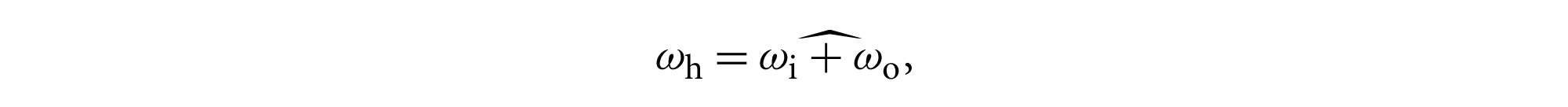
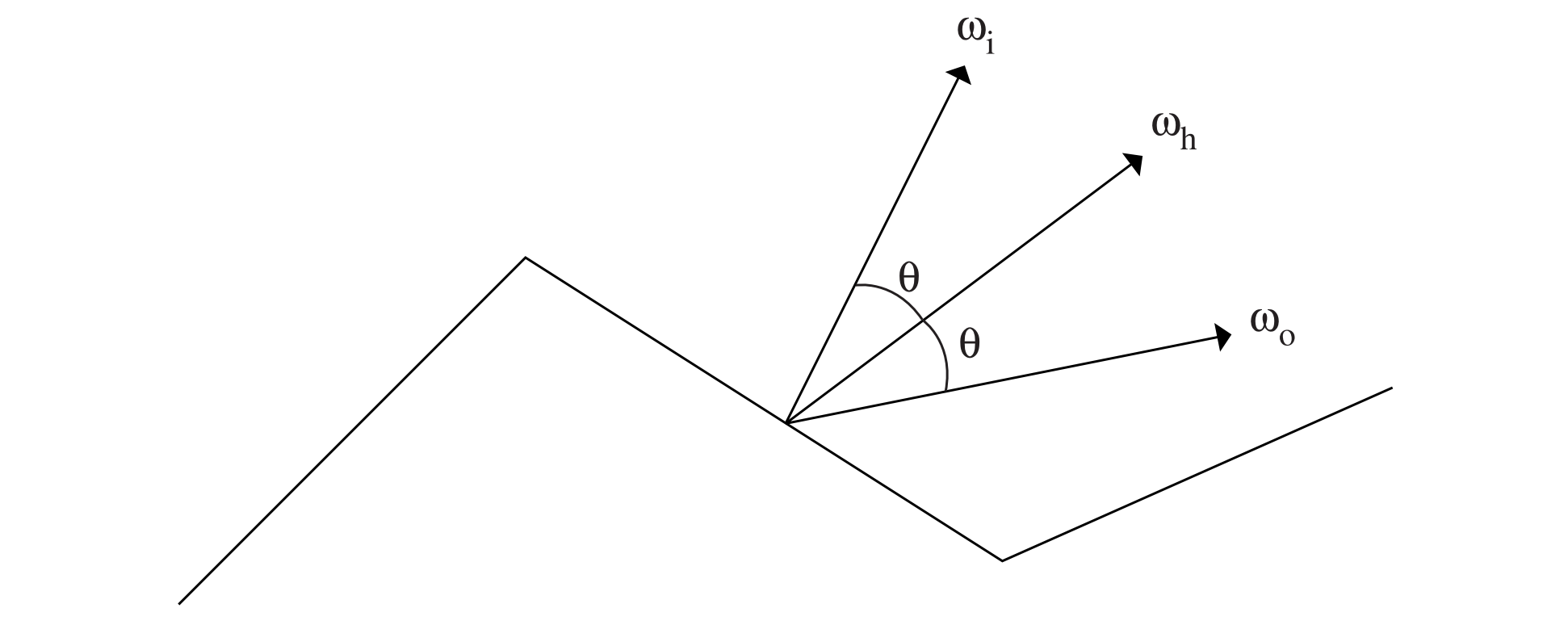
推导如下，各个符号的含义如下图

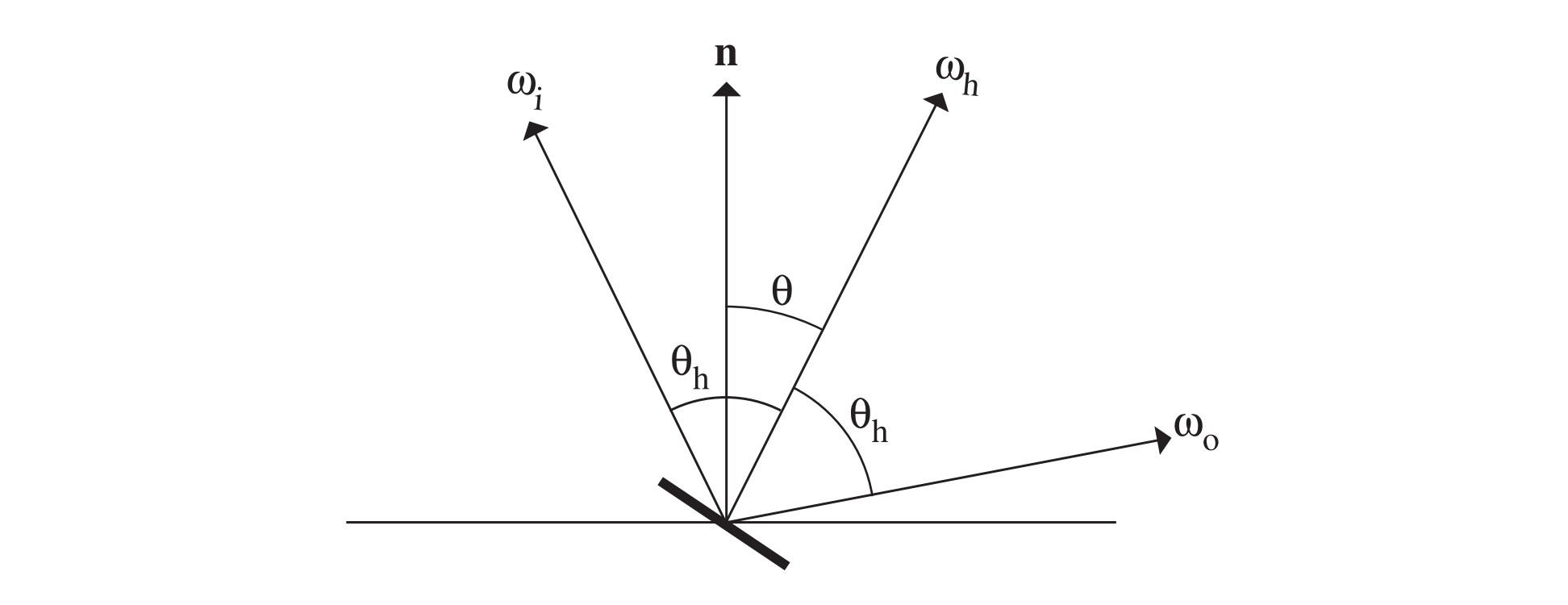
考虑入射微表面的微分通量

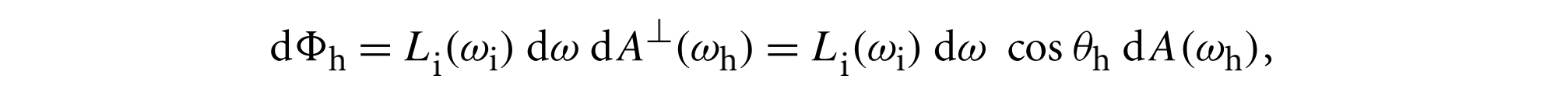
方向为$w_h$的微表面的微分面积为

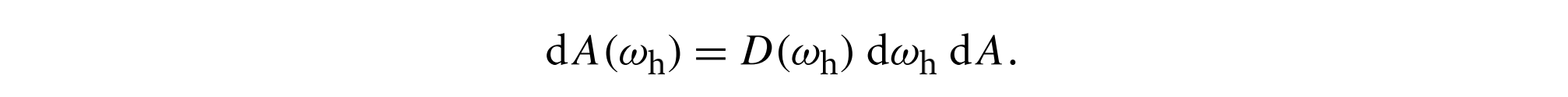
该乘积的前两项描述了每单位面积中，具有正确取向的平面的微分面积

带入前一个式子有

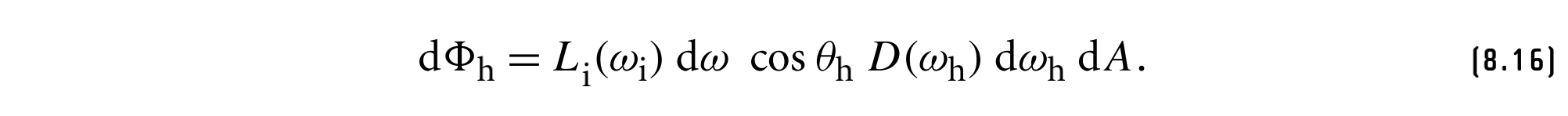
如果我们假设微表面根据菲涅耳定律单独反射光，则出射通量为

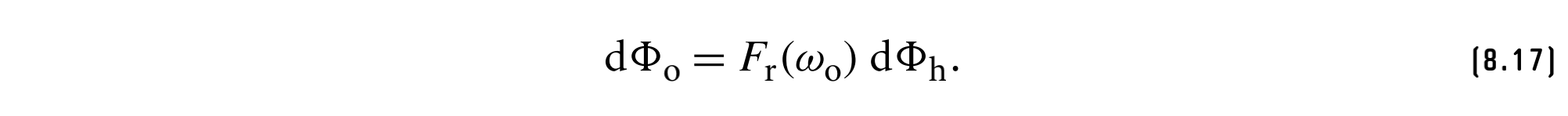
再次使用辐射度的定义，反射出的辐射度为

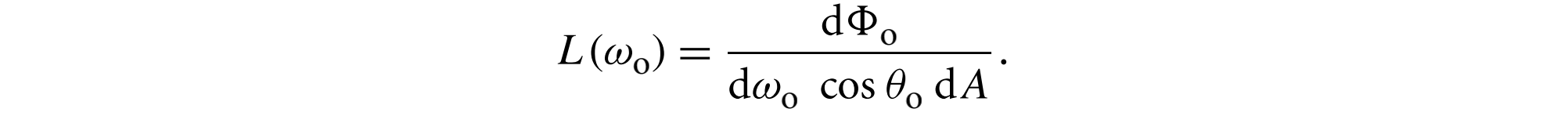
结合等式[8.16],[8.15]有

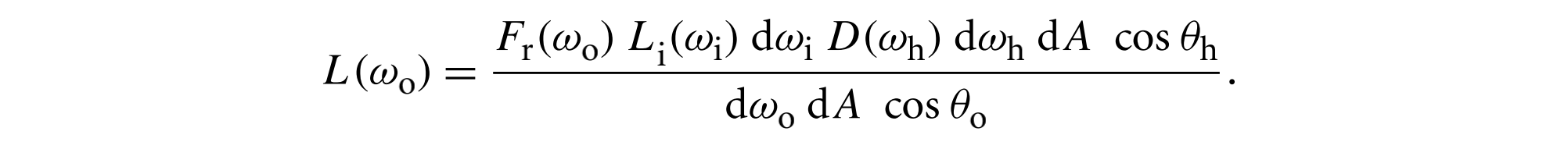
镜面反射下，$dw_h, dw_o$有如下关系(在14章推导)

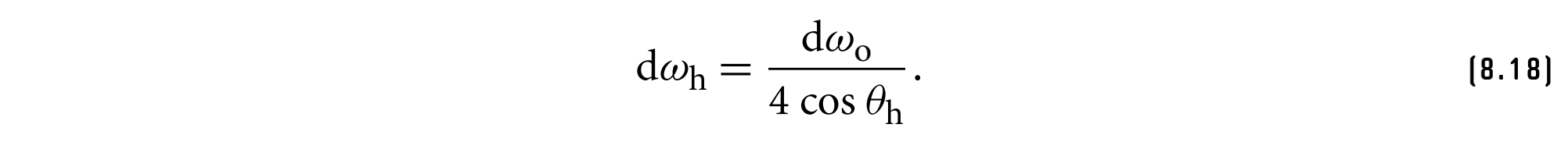
带入前一个方程有

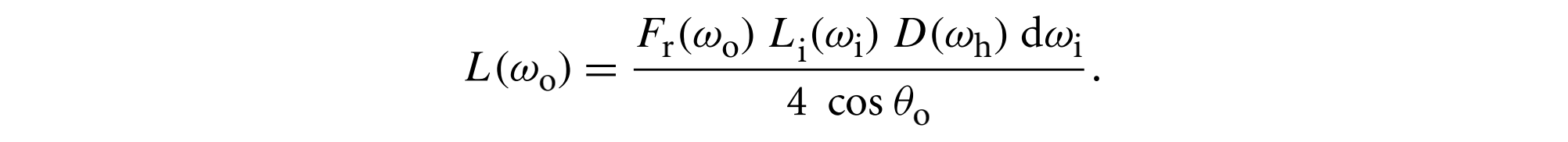
最后，添加几何衰减项$G(w_0, w_i)$，得到Torrance-Sparrow BRDF:

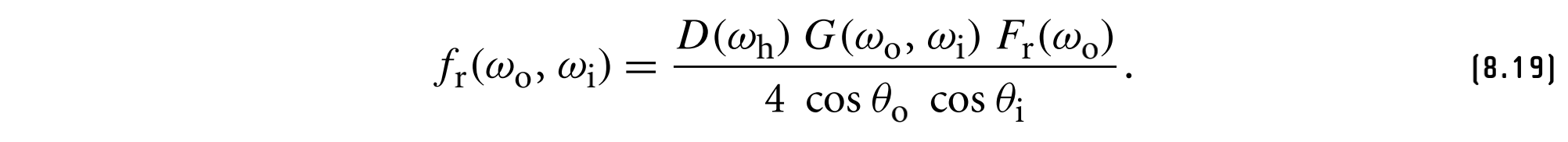
该模型的优点之一是其推导不依赖于所使用的特定微表面分布，也不依赖于具体的菲涅耳函数，因此可以用于导体和电介质

对于BTDF，从折射率为$\eta_i$的介质到折射率为$\eta_o$的介质，其$dw_h$和$dw_o$的关系如下

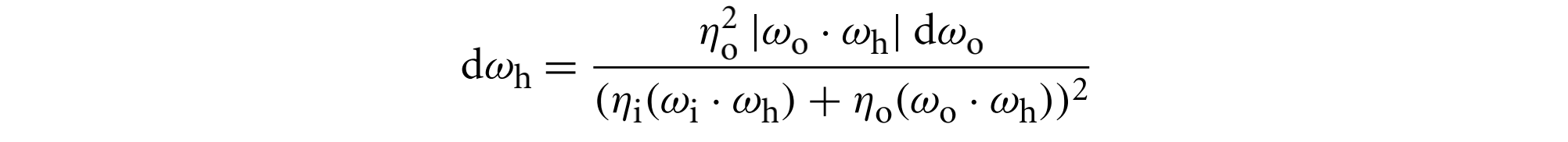
此时的BTDF为

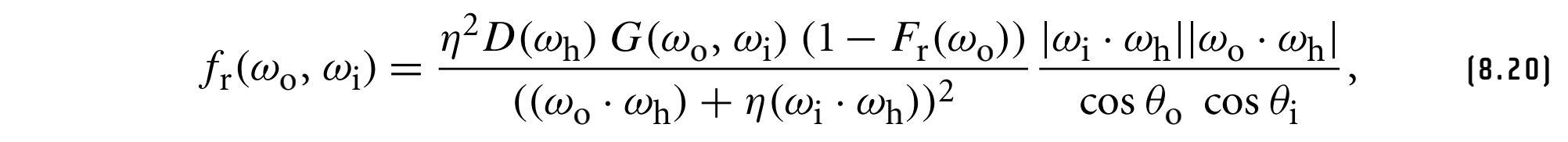
其中$\eta = \eta_i / \eta_o$，对于镜面透射，半角向量为

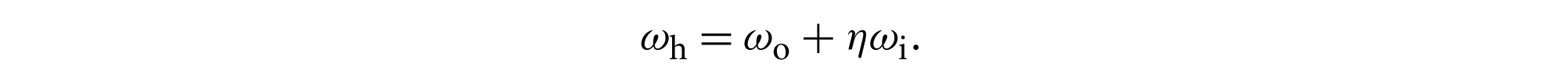
菲涅耳入射效应

假设某个材质的表面是分层的，菲涅耳反射会减少到达分层对象的底层光量，考虑一张抛光的木桌或者涂有光泽油漆的墙壁，如果从正面看过去，主要看到的是本身颜料的颜色，即漫反射的分量；如果从倾斜的角度看过去，则看到的底层颜色较少，此时它被菲涅耳效应引起的更多的光泽反射所覆盖

Ashikhmin和Shirley开发的BRDF模型模拟漫反射底层表面，其上方有光滑的镜面反射表面，漫反射表面的反射效果通过考虑菲涅耳效应后剩余的能量进行分配和调节。当入射光接近法线时，大部分光线透射到漫反射层，此时漫反射项占据主导地位。当入射光接近掠射时，光泽反射成为主要的反射模式

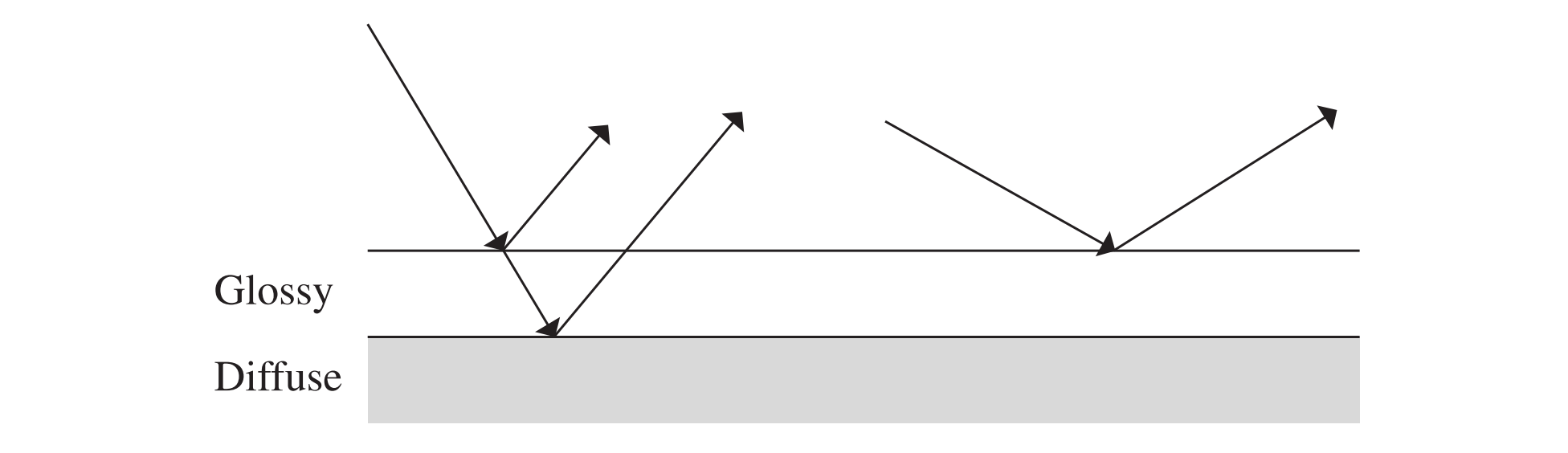
该模型基于光泽镜面反射项和漫反射项的加权和，光泽镜面项导出为

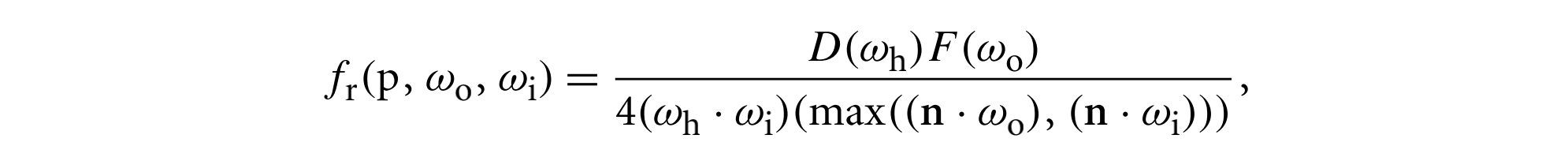
其中$D(w_h)$是微表面分布项，$F(w_o)$代表菲涅耳反射比

Schlick将菲涅耳反射近似为

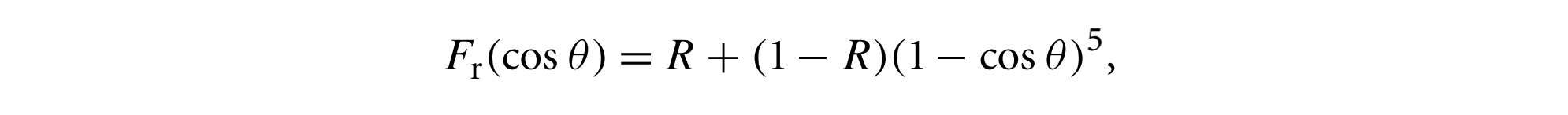
其中$R$是表面在法向入射时的反射率，可以看到，入射角度越大，即视角越倾斜，反射率的值越大，反射所占的分量越多

最后，以下等式中的漫反射项以物理上合理的方式模拟了基于菲涅耳入射效应：

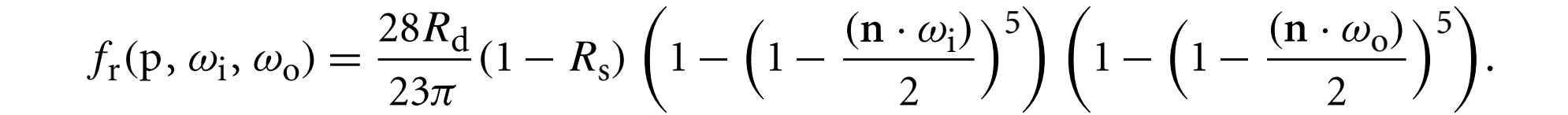
其中，$R_s$是镜面反射的反射率，$R_d$是漫反射的反射率

傅里叶基BSDF

该模型使用傅里叶基表示具有缩放余弦项和的BSDF，对于某些具有逆反射性的材质来说处理较好

其BSDF公式如下：

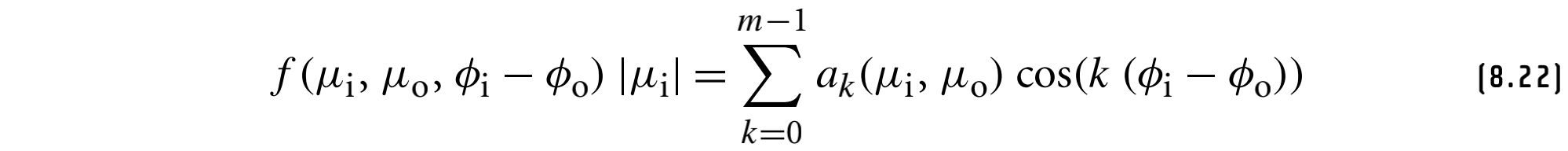
其中，$\mu$是天顶角，$\phi$是方位角，$a_k(\mu_i, \mu_o)$表示一对特定天顶角余弦的傅里叶级数，这主要通过查表来得到

推导以及计算$a_k$的方法见原书8.6节