堆排序&优先队列

堆排序

堆排序原理

堆是一颗具有特定性质的二叉树。
堆的性质：

1. 堆中所有结点的值必须大于或者等于(或小于等于)其孩子结点的值；
2. 堆是一颗完全二叉树。

二叉堆：
在二叉堆中，每个结点最多有两个孩子结点，二叉堆一般分为 二叉最小堆 和 二叉最大堆

堆排序函数

下面以最小堆为例列举实现二叉堆需要的函数

变量声明

//头文件
#include <stdio.h>

#define MAXN 1001

//自定义元素类型
typedef int ElemType;

//最小堆的顺序表
int SizeOfHeap = 0;
ElemType Heap[MAXN];

插入堆函数

先将插入的结点放在二叉树的末尾，然后根据优先级与其双亲结点进行比较，如果优先级高于双亲结点则将他们交换，直到重新形成二叉堆。

void push(ElemType x){
    //首先插入到最后一个位置
    int index = ++SizeOfHeap;
    //向上调整
    while(index > 1){  //只有i>1时才有父节点
        int IndexOfParent = index / 2;
        if(Heap[IndexOfParent] <= x){
            break;
        }
        Heap[index] = Heap[IndexOfParent];
        index = IndexOfParent;
    }
    Heap[index] = x;
}

图解

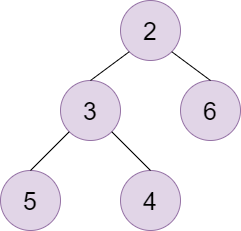
初始堆

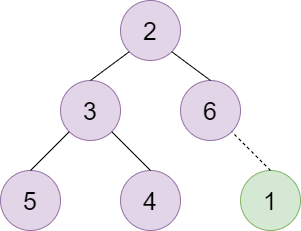
插入新结点并向上调整

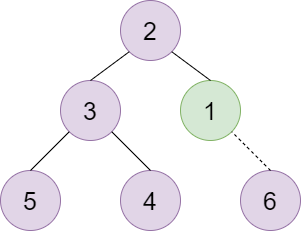
继续向上调整

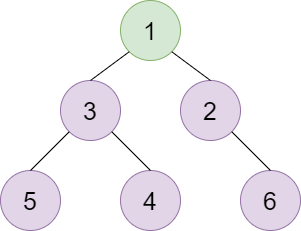
插入完成

删除最值函数

先临时保存一份最值，然后将最后一个结点放到根节点，依次向下移动结点直到二叉堆平衡。

//删除操作
ElemType pop(){
    //获取最值
    ElemType result = Heap[1];
    //相当于将最后一个结点放到根节点
    ElemType x = Heap[SizeOfHeap];
    int index = 1;
    //一定要有子节点
    while(2 * index <= SizeOfHeap){
        int LSonIndex = 2 * index;
        int RSonIndex = 2 * index + 1;
        //比较儿子结点的最值
        int MinIndex = LSonIndex;
        if(RSonIndex <= SizeOfHeap && Heap[RSonIndex] < Heap[MinIndex]){
            MinIndex = RSonIndex;
        }
        //如果没有颠倒就结束
        if(Heap[MinIndex] >= x){
            break;
        }
        Heap[index] = Heap[MinIndex];
        index = MinIndex;
    }
    Heap[index] = x;
    SizeOfHeap--;
    return result;
}

图解

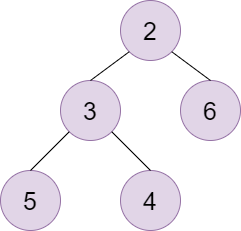
初始堆

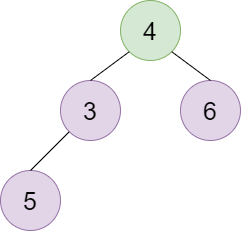
将尾结点移动到根节点

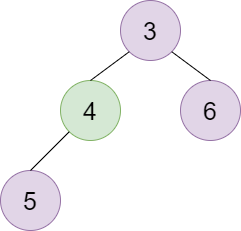
平衡二叉堆

获取堆顶元素

//获取堆顶元素
ElemType GetTop(){
    return Heap[0];
}

创建空堆

使用一个数组来创建空堆

void Build_Heap(int data[],int n){
    //创建一个空堆
    SizeOfHeap = 0;
    for(int i = 0;i < n;i++){
        push(data[i]);
    }
}

优先队列

原理

优先队列也是一种队列，不过优先队列的出队顺序是按照优先级来的

如果最小的键值元素拥有最高的优先级，那么这种优先队列叫做升序优先队列, 相反，如果最大键值元素具有最高的优先级，这种优先队列叫做降序优先队列。

优先队列的基本操作类似于二叉堆的基本操作。

优先队列的应用

• 数据压缩：Huffman 算法
• 最短路径：Dijkstra算法
• 最小生成树：Prim算法
• 事件驱动仿真：顾客排队算法
• 选择问题：查找第k个最小元素
• … …

优先队列的实现比较

实现	插入	删除	寻找最小值
无序数组	1	n	n
无序链表	1	n	n
有序数组	n	1	1
有序链表	n	1	1
二叉搜索树	log n（平均）	log n（平均）	log n（平均）
平衡二叉搜索树	log n	log n	log n
二叉堆	log n	log n	1