最短未排序数组

问题描述

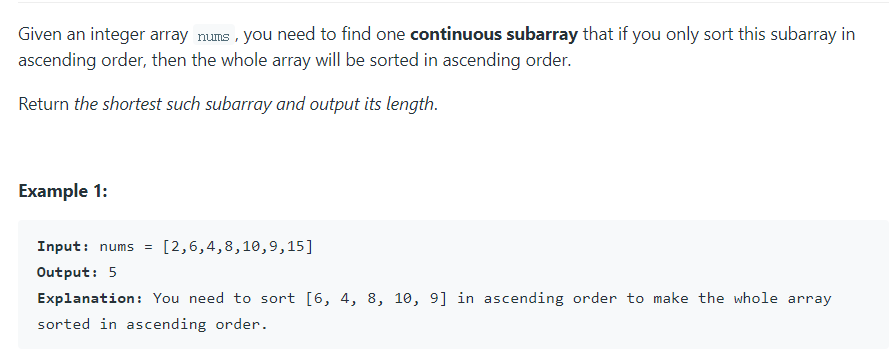
给定一个数组，求它的一个子数组的最短长度，使得该数组完成升序排序后，整个数组也达到升序。

方法1：选择排序思想

模拟选择排序的方法，能够得到每个位置排好序后应该放置的数字，如果这个数字发生了改变，说明这个位置是在所求的子数组内部的，因此通过这种方法能够找到该数组的左边界和右边界，算法复杂度为：时间$O(n^2)$, 空间$O(1)$。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int l = nums.length, r = 0;
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] < nums[i]) {
                    r = Math.max(r, j);
                    l = Math.min(l, i);
                }
            }
        }
        return r - l < 0 ? 0 : r - l + 1;
    }
}

方法2：比对排序数组

如果有足够大的空间，那么该上面的算法可以直接在排好序之后给每个值一一比对，找出发生改变的位置的左边界和右边界，算法复杂度为：时间$O(n)$， 空间$O(n)$。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] snums = nums.clone();
        Arrays.sort(snums);
        int start = snums.length, end = 0;
        for (int i = 0; i < snums.length; i++) {
            if (snums[i] != nums[i]) {
                start = Math.min(start, i);
                end = Math.max(end, i);
            }
        }
        return (end - start >= 0 ? end - start + 1 : 0);
    }
}

方法3：使用栈

下面两种方法都需要考虑的数字进行了筛选，该问题的核心是找到子数组的左边界和右边界。

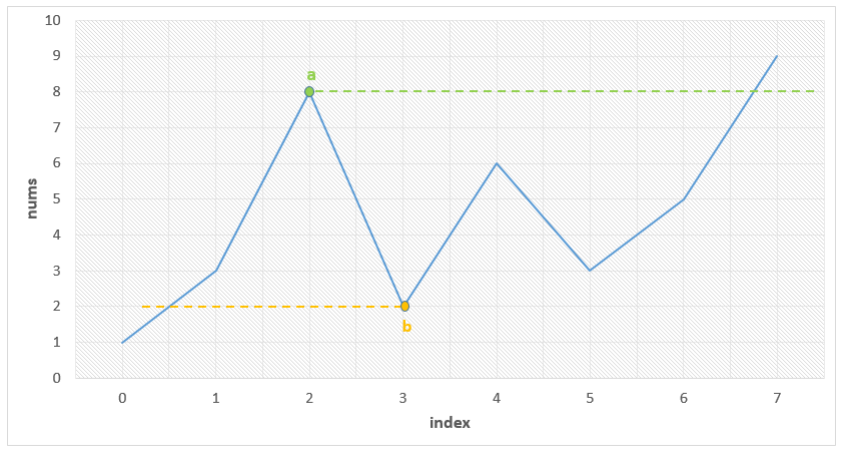
对于左边界而言，在排好序后该位置的数字应该是所有降序区间的数字中最小的那个，因为对于该数字前面的数字，它们的顺序已经是升序，因此不需要进行排列。

右边界同理，只需要把考察的方向更换一下。

这个算法的核心是，如果前面的数字大于当前的数字，则入栈，否则将栈中的元素依次弹出，直到放入前面的元素后栈依然是升序的，此时经过处理得到左边界。右边界同理，该算法的复杂度为：时间$O(n)$, 空间$O(n)$。

public class Solution {
    public int findUnsortedSubarray(int[] nums) {
        Stack < Integer > stack = new Stack < Integer > ();
        int l = nums.length, r = 0;
        for (int i = 0; i < nums.length; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] > nums[i])
                l = Math.min(l, stack.pop());
            stack.push(i);
        }
        stack.clear();
        for (int i = nums.length - 1; i >= 0; i--) {
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i])
                r = Math.max(r, stack.pop());
            stack.push(i);
        }
        return r - l > 0 ? r - l + 1 : 0;
    }
}

方法4：找特殊极值（最优）

解决问题的核心方法同上，但是不需要使用栈来处理了，因为直接可以直接通过比大小的方式得到左右边界的值。

复杂度: 时间$O(n)$, 空间$O(1)$。

public Solution{
    public int findUnsortedSubarray(int[] sums){
    	int l = 0, r = nums.length - 1;
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        int st = 0, nd = -1;
        while(r >= 0){
            if(nums[l] >= max){
                max = nums[l];
            } else {
                nd = l;
            }
            if(nums[r] <= min){
                min = nums[r];
            } else {
                st = r;
            }
            l++;
            r--;
        }
        return nd - st + 1;
	}
}