栈&递归&深度优先搜索

栈&递归&深度优先搜索

栈

栈是一种支持先进后出的数据存储结构，也是一种最常见的数据结构。对于一个栈来说，我们只能每次从栈顶压入元素，或者从栈顶取出元素，而内部的其他数据对外是不可访问的。栈一般分为顺序栈和链式栈。

一般用法是，栈最初是空的，栈顶指向NULL或者-1, 当需要有元素压入栈时，则开辟一片新的空间（顺序栈就是当前栈顶的下一个位置），然后将栈顶指之；出栈时，先将该元素赋给其他的值或者销毁（顺序栈可略过），然后移动栈顶指针至前一个元素。

注意：只有栈不满时才能入栈，只有栈不空时才能出栈。在解决实际问题时，如果push 和pop的算法并没有检查栈顶的位置，很容易造成越界！

顺序栈

以数组的形式存储数据的栈，除了方便查找以外并没有其他优点（但是一般情况下栈结构是不允许查找栈顶以外元素的），但是如果临时使用栈的话，顺序栈写起来不会十分麻烦，一般常用于小规模使用。缺点就是栈的空间具有限制。

顺序栈的实现

一般情况下，顺序栈只需要一个数组和一个记录栈顶下标的变量就能实现，比较规范的写法如下。

文件：sq_stack.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//从顺序栈开始写起
//顺序栈没有别的优势，就是好写，o(╥﹏╥)o，同时如果突然改需求成链表
//就不用查找那么麻烦
//现在开始吧(*^▽^*)

//先定义基本数据类型
typedef int ElemType;

#define MAX_SIZE 500

typedef struct node{
    int top;
    ElemType stack[MAX_SIZE];
}Stack;

//基本操作
int init_sq_stack(Stack **st);
int is_empty(Stack *st);
int push(Stack *st, ElemType *x);
int pop(Stack *st);
int get_top(Stack *st,ElemType *x);
int destory_sq_stack(Stack **st);

文件：sq_stack.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "sq_stack.h"

//基本操作
int init_sq_stack(Stack **st){
    *st = (Stack*)malloc(sizeof(Stack));
    (*st)->top = -1;
    memset((*st)->stack, 0, sizeof((*st)->stack));
    return 1;
}
int is_empty(Stack *st){
    return st->top == -1;
}
int push(Stack *st, ElemType *x){
    if(st->top == MAX_SIZE - 1){
        perror("The stack is full!\n");
        return 0;
    }
    st->top++;
    st->stack[st->top] = (*x);
    return 1;
}
int pop(Stack *st){
    if(is_empty(st)){
        perror("The stack is empty!\n");
        return 0;
    }
    st->top--;
    return 1;
}
int get_top(Stack *st,ElemType *x){
    if(is_empty(st)){
        perror("The stack is empty!\n");
        return 0;
    }
    (*x) = st->stack[st->top];
    return 1;
}

int destory_sq_stack(Stack **st){
    free(*st);
    (*st) = NULL;
}

链式栈

链式栈是实现栈的比较理想的存储方式，它不受空间限制。为了方便出栈，链式栈中的结点一般指向它的前一个结点，而栈空时，头结点指向NULL。

链式栈的实现

link_stack

链式栈的基本结构

文件：link_stack.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

//链式栈不受空间的约束，是一种比较理想的栈的结构
typedef int ElemType;

typedef struct node{
    ElemType data;
    struct node *last;
}StNode;

typedef struct stack{
    struct node *top;
    int size;
}Stack;

int init_stack(Stack **st);
int is_empty(Stack *st);
int push(Stack *st, ElemType *x);
int pop(Stack *st);
int get_top(Stack *st,ElemType *x);
int destory_stack(Stack **st);
int get_size(Stack *st);

文件：link_stack.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <stdio.h>
#include <stdlib.h>
#include <stdlib.h>
#include "link_stack.h"

int init_stack(Stack **st){
    *st = (Stack *)malloc(sizeof(Stack));
    (*st)->size = 0;
    (*st)->top = NULL;
    return 1;
}
int is_empty(Stack *st){
    return st->top == NULL;
}
int push(Stack *st, ElemType *x){
    StNode *s = (StNode *)malloc(sizeof(StNode));
    s->data = (*x);
    s->last = st->top;
    st->top = s;
    st->size++;
    return 1;
}
int pop(Stack *st){
    if(is_empty(st)){
        perror("The stack is empty!\n");
        exit(1);
    }
    StNode *tmp = st->top;
    st->top = tmp->last;
    free(tmp);
    st->size--;
    return 1;
}
int get_top(Stack *st,ElemType *x){
    if(is_empty(st)){
        perror("The stack is empty!\n");
        exit(1);
    }
    (*x) = st->top->data;
    return 1;
}
int destory_stack(Stack **st){
    while((*st)->top != NULL){
        pop(*st);
    }
    free(*st);
    (*st) = NULL;
    return 1;
}
int get_size(Stack *st){
    return st->size;
}

递归

原理

在定义一个过程或者函数时出现调用本过程或 本函数的成分称为递归，调用自身为直接递归，比如二叉树中的先序遍历，图中的深度优先搜索；调用其他函数称为间接递归，比如快速排序。

如果一个递归过程或递归函数中的递归调用语句是最后一条执行语句，则称这种递归调用为尾递归，比如阶乘算法。

一般情况下， 一个递归模型由递归出口和递归体两部分组成，在实际算法中也就是要解决这两个东西。

举个例子，在阶乘算法中，n == 1 就是递归出口，当递归深入到这一层时就需要返回，而递归体就是 $ f(n) = n * f(n - 1) $，程序通过该递归体一步步向下递推，直到 遇到n == 1的情况时返回，最后依照原先的路径一步步回归到 $ n == n_0 $就完成了本次递归。

递归的本质应该是广义上的数学归纳法，即结构归纳法，在知道已知条件$ K_0 $的情况下，通过假设$ Ki $成立推导出$ K_(i + 1) $成立，完成证明。递归因此也是将大问题转化成若干个小问题的过程。

递归与非递归的转换

​ 因为递归依然是通过调用系统栈来实现的，所以本质上，只要记录下递归过程中的参数和返回值，就能够自己用栈来模拟递归过程。

一般情况下，尾递归算法能够通过循环或者迭代的方式转换为等价的非递归算法，例如求Fibonacci数列的非递归算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
int Fib(int n){
    int a = 1, b = 1, i, s;
    if(n == 1 || n == 2){
        return 1;
    } else {
        for(i = 3;i <= n;i++){
            s = a + b;
            a = b;
            b = s;
        }
        return s;
    }
}

而对于非尾递归的算法，可以通过栈来模拟递归执行过程，从而将其转化为等价的非递归算法。

最典型递归算法的莫过于汉诺塔原理，几乎讲到递归就会涉及它。先贴出一份递归写法。

1
2
3
4
5
6
7
8
void Hanoi(int n, char X, char Y, char Z){
    if(n == 1)printf("%c -> %c\n",X, Z);
    else {
        Hanoi(n - 1, X, Z, Y);
        printf("%c -> %c\n", X, Z);
        Hanoi(n - 1, Y, X, Z);
    }
}

​ 非递归的实现：需要使用一个栈来暂时存放还不能直接移动盘片的任务/子任务。

大概的思路是，先将任务Hanoi(n, x, y, z)进栈，栈不空是循环：出栈一个任务Hanoi(n, x, y, z)，如果它是可以直接移动的， 就移动盘片；否则将该任务转化为Hanoi(n - 1, x, z, y)，move(n, x, z) , Hanoi(n - 1, y , x, z)，按相反顺序依次进栈， 其中move(n, x, z)是可以直接移动的任务，相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
typedef struct{
    int n;   //盘片个数
    char x, y, z;
    int flag;   //可直接移动时为1，否则为0
}ElemType;

typedef struct{
	ElemType data[MaxSize];
    int top;
}StackType;

void InitElem(ElemType *e, int n, char x, char y, char z, int flag){
    e->n = n; e->x = x; e->y = y; e->z = z; e->flag = flag;
    return;
}

void Hanoi(int n, char x, char y, char z){
    StackType *st;
    ElemType e, e1, e2, e3;
    if(n <= 0)return;
    InitStack(st);
    InitElem(&e, n, x, y, z, 0);
    push(st, e);
    while(!StackEmpty(st)){
        pop(st, e);
        if(e.flag == 0){
            InitElem(&e1, e.n - 1, e.y, e.x, e.z, 0);
            if(e1.n == 1){
                e1.flag = 1;
            } else e1.flag = 0;
            push(st, e1);
            InitElem(&e2, e.n, e.x ,e.y, e.z, 1);
            push(st, e2);
            InitElem(&e3, e.n - 1, e.x, e.z, e.y, 0);
            if(e3.n == 1){
                e3.flag = 1;
            } else e3.flag = 0;
            push(st, e3);
        } else {
            printf("%c -> %c\n",e.x, e.z);
        }
    }
    DestroyStack(st);
}

深度优先搜索

图中的DFS

  • 原理

    ​ 深度优先遍历的过程是从图中的某个初始点v出发，首先访问初始点v，然后选择一个与v相邻的且没有被访问过的顶点w，以w为初始顶点，再从它出发进行深度优先遍历，直到图中与顶点v邻接的所有顶点都被访问过为止，一般通过递归来实现。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    int visited[max] = {0};//全局数组，判断结点是否被访问过
    void DFS(AdjGraph *G, int v){
        ArcNode *p;
        visited[v] = 1;
        print("%d",v);
        p = G->adjlist[v].firstarc;
        while(p != NULL){
            if(visited[p->adjvex] == 0){
                DFS(G, p->adjvex);
            } p = p->nextarc;
        }
    }

  • 应用

    1. 判断两点之间是否有最短路径
    2. 求出最大连通图的数量
    3. 拓扑排序（需要借助post实现）
    4. 求两点之间的所有路径（回溯）

广义DFS

相较于限制在图中的DFS，广义上的DFS能够解决更多，更普遍的问题。

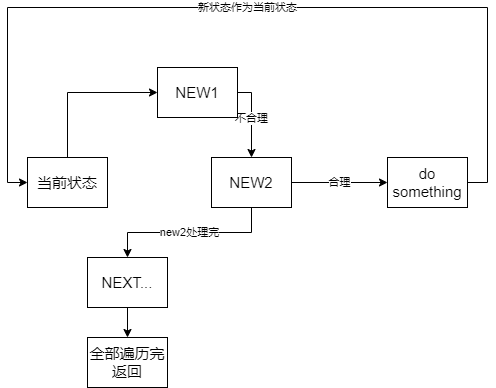
DFS和枚举类似，都是一种很朴素自然的遍历方法。当我们遇到一种状态之后，我们开始判断它产生（或连接）的所有合理的新状态，每遇到一个新状态便递归使用DFS访问它，直到该状态下的所有情况访问完，该算法结束。

dfs_flow

模板1(递归实现):

1
2
3
4
5
6
7
DFS function(params: current node, target node, hash_table visited):
	if cur == target: return true
	for every suitable neighbor in current node's neighbors:
		add each to visited
		if DFS(each, target, visited): return true
	//if not find target
	return false

模板2(栈实现):

1
2
3
4
5
6
7
8
9
10
11
12
13
DFS function(params: root node, target node):
	hash_table visited
	init stack  //store nodes that not finished yet
	add root to stack
	while stack not empty:
		current node = top of stack
		remove top elem in stack
		if cur == target: return true
		for every suitable neighbor in cur node's neighbors:
			add each to visited
			add each to stack
	//if not find target
	return false
数据结构与算法
#DFS #栈 #递归
栈&递归&深度优先搜索
http://example.com/2023/01/10/栈&递归&深度优先搜索/
作者
Chen Shuwen
发布于
2023年1月10日
许可协议