组合数

要求

给出两个整数n和k, 返回1~n 的所有k 个组合数

eg:

n = 4, k = 2

answer: [ [2,4], [3,4], [2, 3], [1, 2], [1, 3], [1, 4] ], 共6种情况

解决思路

解法一：DFS

考虑深度优先算法，先在当前序列中任取一个数字，然后与其后的子序列形成的组合数再进行组合，例如，对于序列14，当需要求2个数的组合时，先选取一个数为1，然后在23中再取一个数与其进行组合，得到1,2 1,3 1,4 。再取第一个数为2， 同理得到2,3 2,4 。最后取第一个数为3，得到3,4 。此时剩余的数字的个数小于2（此处只有一个数字4），问题解决。

//k为需要组合的数字的个数，s为需要组合的序列的起点，ans存放结果，tmp临时存放生成的序列
void DFS(int k, int s, int n, vector<vector<int>> &ans, vector<int> tmp){
    if(k == 0){//如果拿取的数字达到要求，将生成序列放入答案中
        ans.push_back(tmp);
        return;
    }
    for(int i = s; i <= n; i++){
        if(n - i + 1 < k)break;//如果剩余的数字个数小于还需拿取的数字个数，则该种情况Pass
        tmp.push_back(i);
        DFS(k - 1, i + 1, n, ans, tmp);//对剩下的序列进行组合。
        tmp.pop_back();
    }
    return;
}

vector<vector<int>> combine(int n, int k){
    vector<vector<int>> ans;
    DFS(k, 1, n, ans, vector<int>());
    return ans;
}

解法二：动态规划

先找到所求函数的转移方程，这里用到高中所学的公式：
$$
C_{N}^{M} = C_{N - 1}^{M - 1} + C_{N - 1}^{M}
$$
意思就是说，要找到N个数的组合数，可以先找到N-1个数中不含N的组合数，再找到N-1个数中含N的组合数。

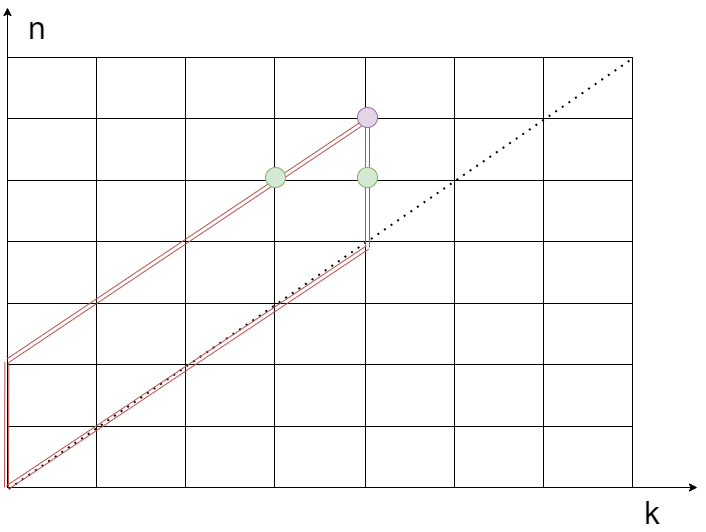
此时需要寻找所求n,k之间的关系，我们把两个变量放入二维坐标系中就能比较清楚的看出循环思路，如图：

假设图中紫色的点代表待求的最终关于n和k的组合数，则需要先求出两个绿色点处的组合数，然后让左边点求出的组合数添加上数n后，再和右边点求出的组合数结合起来就是最终结果。以此类推，我们需要求的点为图中红色边框内的所有点，为了使临时存放的值尽可能少，我们可以制定以下策略：

先从左向右求出n = k + b上每个点代表的组合数（内部循环），这样，利用当前斜线上的前一个点和上一条线上相同横坐标的点再求n = k + b + 1, n = k + b + 2, … , n = k + b + a上的点（外层循环），求出的最后一个点即为答案。该算法的时间复杂度为$O(n^2)$, 空间复杂度为$O(n)$。

vector<vector<int>> combinations(int n, int k){
    if(k == 0)return vector<vector<int>>();//k = 0比较特殊，可以拿出来单独讨论
    vector<vector<int>> *combs = new vector<vector<int>>[k+1];
    int startN = 0; //外层循环的变量
    int increment;  //内层循环的变量
    while(startN <= n - k){
        increment = 1;
        while(increment <= k){
            if(increment == 1){//k=1，代表从1-n中任取一个值
                combs[increment].clear();
                for(int i = 1; i <= startN + increment; i++)
                    combs[increment].push_back(vector<int>(1, i));
            } else if(increment == startN + increment){//n个数中拿取n个数，组合数为它自身
                vector<int> comb;
                for(int i = 1; i <= increment; i++){
                    comb.push_back(i);
                }
                combs[increment].push_back(comb);
            } else {
                int curN = startN + increment;
                vector<vector<int>> lastComb = combs[increment - 1];
                //上个点的组合数再添加上数n
                for(auto it = lastComb.begin(); it != lastComb.end(); it++){
                    it->push_back(curN);
                    combs[increment].push_back(*it);
                }
            }
            increment++;
        }
        startN++;
    }
    vector<vector<int>> ans = combs[k];
    delete[] combs;
    return ans;
}