逆向分析-除法优化MagicNumber算法逆向

背景

在汇编指令中，除法运算一般使用有符号除法指令idiv或者无符号除法指令div。但是，除法指令的执行周期较长，效率较低，因此编译器会想办法用其他执行周期短的指令来等效替代除法指令。

在C/C++中，除法运算不会保留余数，如果要计算余数可以通过取模运算获得。对于整数除法，C/C++只会保留整数部分，且为向0取整。

C/C++除法规定：

两个无符号整数相除，结果仍然是无符号

两个有符号整数相除，结果仍然是有符号

无符号和有符号混除，有符号数的最高位被当作数据位参与无符号运算，结果为无符号数

当除数为常数时，编译器可以根据4种情况对除法进行优化：

• 除数为正的2的幂
• 除数为负的2的幂
• 除数为正的非2的幂
• 除数为负的非2的幂

其中，后2种情况的除法优化会需要计算Magic Number，本文分析了C2.dll计算Magic Number部分的反汇编代码。C2.dll是VC++编译器下的一个动态库，其中包含了编译C/C++文件用到的函数，用到的版本为12.0.9782.0

过程

定位代码地址

使用PEView打开C2.dll文件，根据已知信息，待逆向代码的文件位置在0x1075FACE处，而.text节的PointertoRawData=0x2000, RVA=0x1000, 如下图所示：

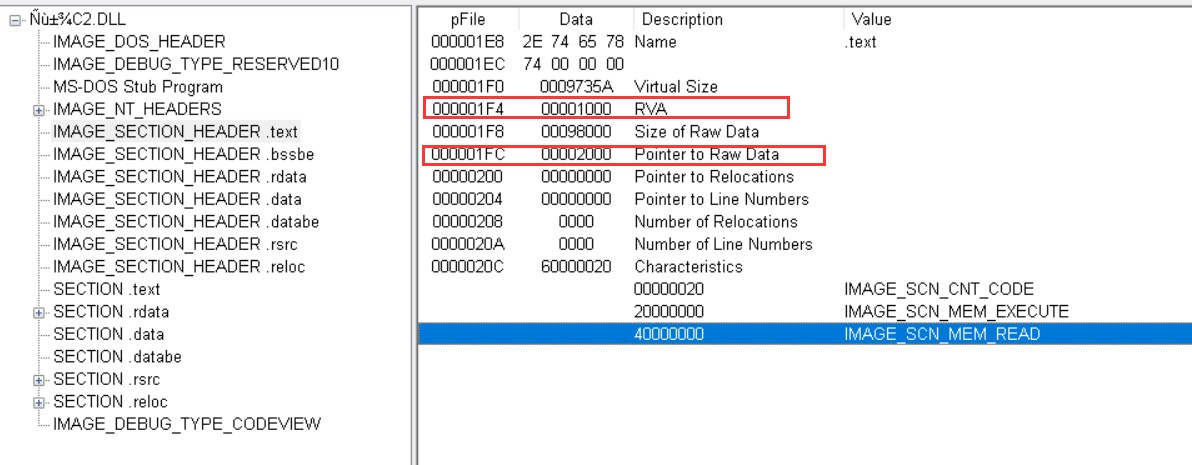
因此代码的虚拟地址为0x1075FACE + 0x1000 - 0x2000 = 0x1075EACE，接下来就可以使用IDA定位到该地址进行逆向分析

代码行为分析

函数从地址0x1075EACE处开始执行，函数的开头如下：

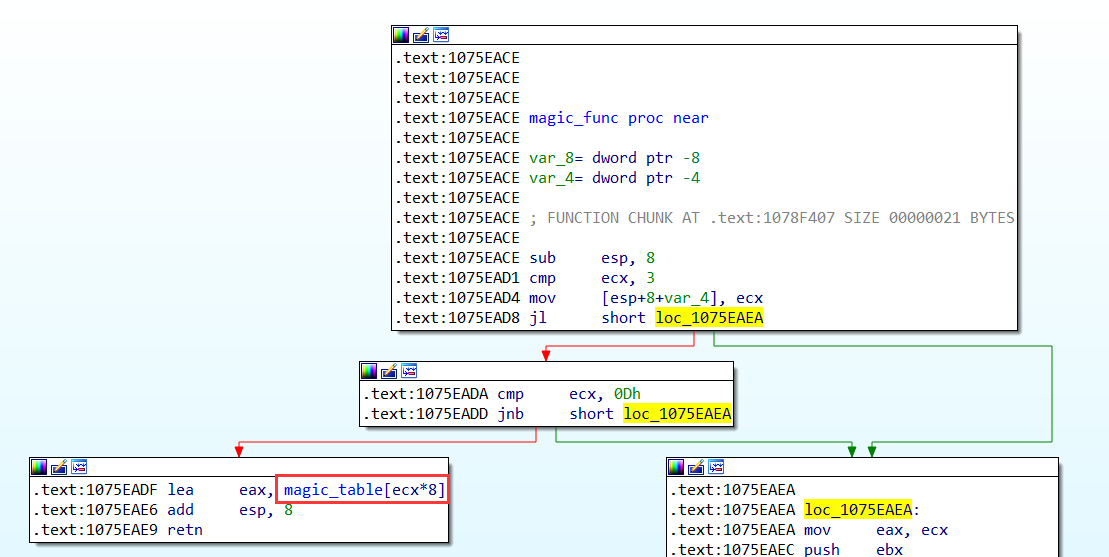
在函数的入口，函数为两个4字节类型的局部变量申请了空间，在地址0x1075EAD1处，函数直接使用了ecx寄存器，说明函数调用约定为__fastcall, 且首个参数为4字节大小。该参数紧接着进行了2次大小比较，在最左边的分支中，函数直接返回了magic_table[ecx * 8]的地址，从该指令可以猜测函数的返回值为一个大小8字节的结构体的地址，查看magic_table处的内容，发现该地址位于全局数据区：

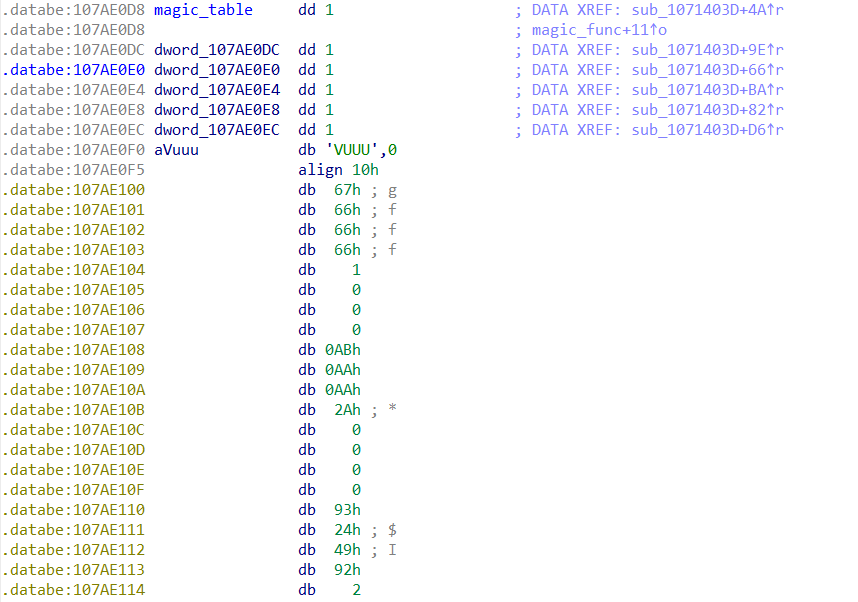
分析该地址处的数组，发现数据确实大概按照4字节进行对齐排列，符合之前的猜测

接着分析右边的分支代码，在地址0x1075EAEF处，发现类似于求绝对值的代码块

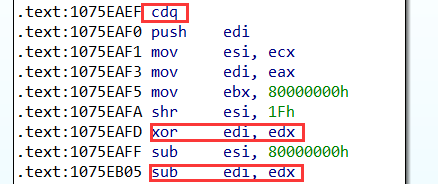
之后函数进行了一些除法和取模的运算，然后进入循环体，其中，跳出循环体的代码主要在以下部分：

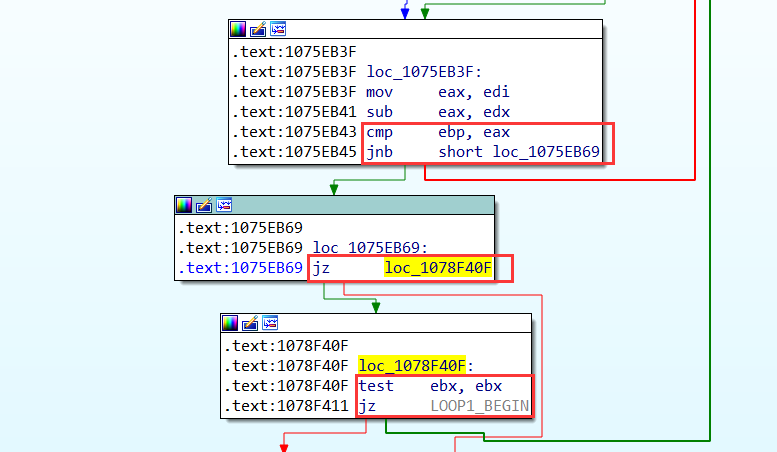
只有满足这3处跳转指令才能够继续循环，猜测while的判断部分为比较复杂的逻辑表达式

而在循环体内，代码包含一些分支结构和简单的四则运算，猜测和算法本身有关。

在函数的最后，代码修改了dword_1079F090处的数据，且将其地址作为返回值：

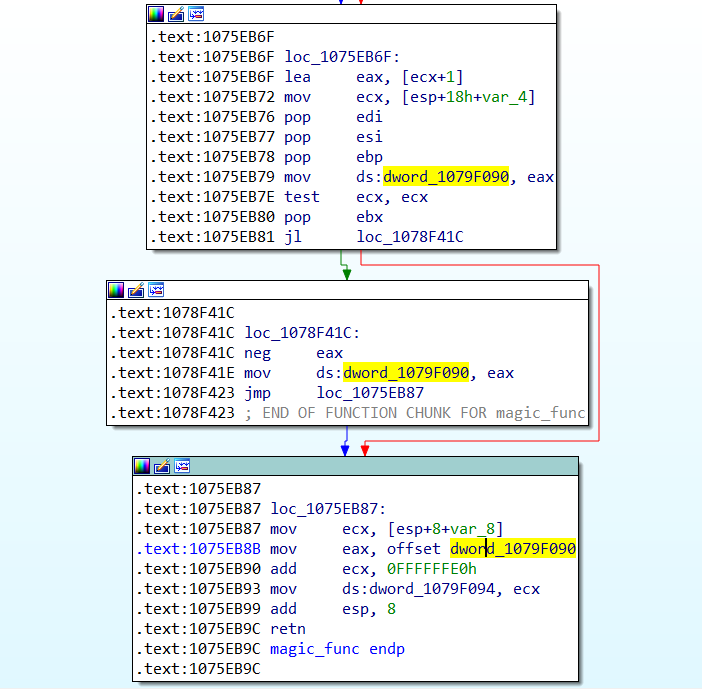
跳转到相应地址处发现，该变量为全局变量：

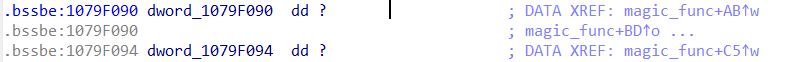
进一步分析可知，在地址0x1075EB93处，该变量的后4个字节也被修改了，回顾函数在第一个跳转分支中同样返回了一个大小为8字节的结构体的地址，可以猜测这个全局变量的大小也为8字节

分析小结

被访问自定义结构体：包含两个4字节变量

被访问全局数组：元素类型为上述结构体

函数参数：1个，大小为4字节

函数返回值：结构体地址

推断函数行为：使用除数计算MagicNumber以及指数的幂（见算法部分），然后封装成结构体返回

算法逆向

阶段一

根据汇编指令，比较初步地还原出算法全过程

根据代码行为还原出的MagicInfo结构：

struct MagicInfo
{
	int magicNumber;
	int expInc;
};

根据全局变量还原出的MagicInfo速查表，其主要用于快速计算除数较小的MagicNumber：

struct MagicInfo g_MagicInfoArray[] = {
  {1, 1},           // 0 
  {1, 1},           // 1
  {1, 1},           // 2
  {0x55555556, 0},
  {0, 0},           // 4
  {0x66666667, 1},
  {0x2AAAAAAB, 0},
  {0x92492493, 2},
  {0, 0},           // 8
  {0x38E38E39, 1},
  {0x66666667, 2},
  {0x2E8BA2E9, 1},
  {0x2AAAAAAB, 1}
};

对算法直接还原后得到的代码如下：

struct MagicInfo g_result;

struct MagicInfo* CalculateMagicInfoOrigin(int divisor) {
	int p = 31;
	int var_4 = divisor;
	// ecx: divisor
	// edx: pExpInc
	if (divisor >= 3 && divisor < 13) {
		return &g_MagicInfoArray[divisor];
	}
	// loc_1075EAEA
	// eax <- divisor
	// cdq: edx = eax >> 31(SIGN)
	// edi <- eax
	// xor edi, edx
	// sub edi, edx
	// edi: absDivisor
	unsigned int eax1;
	unsigned int esi1;
	unsigned int absDivisor;
	unsigned int ebp1, ebx1, ecx1, edx1;

	absDivisor = abs(divisor);
	esi1 = ((unsigned)divisor >> 31) - EXP31;	// nLargestMultiple

	eax1 =  esi1 / absDivisor;		// div edi 
	esi1 = esi1 - esi1 % absDivisor;	// sub esi, edx
	esi1--;

	eax1 =  EXP31 / esi1;				// div esi		// q1


	ebp1 = eax1;					// mov ebp, eax	//q1
	eax1 = (int)eax1 * (int)esi1;					// imul eax, esi
	ebx1 = EXP31;
	ebx1 -= eax1;						// r1

	eax1 = EXP31 / absDivisor;					// div edi	// nMagicNumber

	ecx1 = eax1;
	eax1 = (int)eax1 * (int)absDivisor;			// imul eax, edi
	edx1 = EXP31 - eax1;				// sub edx, eax

	// loc_1075EB47
	// LOOP_BEGIN
	do {
		// mov eax, var_8
		// inc eax
		//eax1 = var_8 + 1;
		p += 1;
		ebx1 = ebx1 + ebx1;			// add ebx, ebx
		ebp1 = ebp1 + ebp1;

		//var_8 = eax1;
		if (ebx1 >= esi1) {
			// loc_1078F407
			ebp1++;
			ebx1 -= esi1;
		}
		// loc_1075EB5C
		edx1 += edx1;
		ecx1 += ecx1;
		if (edx1 >= absDivisor) {	//	cmp edx, edi
			ecx1++;
			edx1 -= absDivisor;
		}
		// loc_1075EB3F
		eax1 = absDivisor;
		eax1 -= edx1;
		//if (ebp1 < eax1)goto LOOP_BEGIN;
		//if (ebp1 == eax1) {
		//	// loc_1078F40F
		//	if (ebx1 == 0)goto LOOP_BEGIN;
		//	break;
		//}
	} while ((ebp1 < eax1) || (ebp1 == eax1 && ebx1 == 0));
	// loc_1075EB6F
	eax1 = ecx1 + 1;
	ecx1 = var_4;
	g_result.magicNumber = eax1;	// mov ds:dword_1079F090, eax
	if((int)ecx1 < 0) {
		// loc_1078F41C
		eax1 = -(int)eax1;
		g_result.magicNumber = eax1; // mov ds : dword_1079F090, eax
	}
	// loc_1075EB87
	ecx1 = p;
	// eax1 = (int) & g_result; //mov eax, offset dword_1079F090;
	ecx1 += -32; //0x0FFFFFFE0
	g_result.expInc = ecx1; // mov ds : dword_1079F094, ecx
	return &g_result;
}

阶段二

对代码进行整理，提取出关键变量并给其命名，对部分冗余的指令进行合并：

struct MagicInfo g_result;

struct MagicInfo* CalculateMagicInfo(int divisor) {
	int p = 31;
	if (divisor >= 3 && divisor < 13) {
		return &g_MagicInfoArray[divisor];
	}

	unsigned int q1, r1, q2, r2, nc, delta, absDivisor;

	absDivisor = abs(divisor);
	nc = ((unsigned)divisor >> 31) - EXP31;
	nc = nc - nc % absDivisor - 1;
	q1 = EXP31 / nc;
	r1 = EXP31 % nc;
	q2 = EXP31 / absDivisor;
	r2 = EXP31 % absDivisor;
	do {
		p += 1;
		r1 *= 2;
		q1 *= 2;
		if (r1 >= nc){
			q1 += 1;
			r1 -= nc;
		}
		r2 *= 2;
		q2 *= 2;
		if (r2 >= absDivisor) {
			q2 += 1;
			r2 -= absDivisor;
		}
		delta = absDivisor - r2;
	} while ((q1 < delta) || (q1 == delta && r1 == 0));

	g_result.magicNumber = q2 + 1;
	if (divisor < 0) {
		g_result.magicNumber = -g_result.magicNumber;//~(q2 + 1) + 1;
	}

	g_result.expInc = p - 32;
	return &g_result;
}

MagicNumber正确性验证

判断逆向的算法是否正确，最好的办法就是将”赝品“和真品直接进行比较。本文中，我通过动态加载C2.dll函数库，直接调用计算Magic Number的原函数，并验证了整型范围内的所有除数输入，结果证明，两者的输出是一模一样的

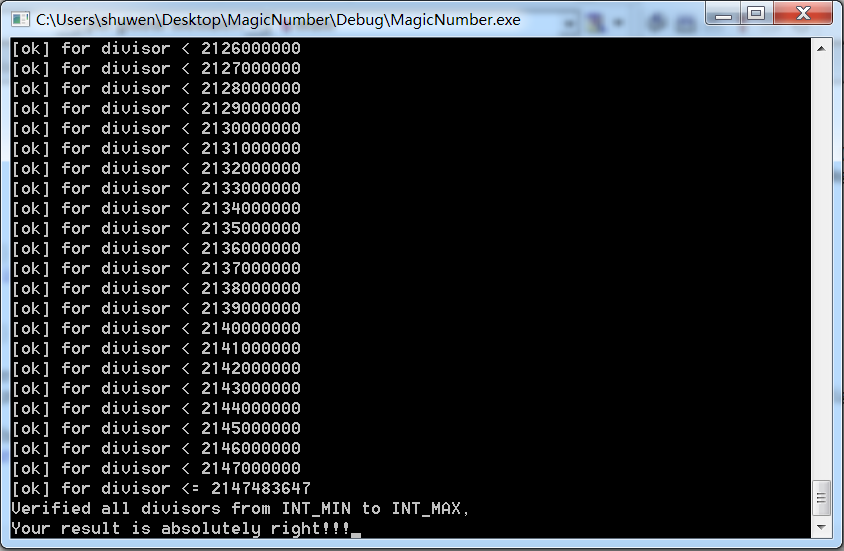
除法正确性验证

本文又测试了INT_MIN除以所有整型的结果并和原结果进行比较，两者的输出同样是一模一样的

验证代码见源项目。

算法证明

本文只讨论有符号数除法的优化中MagicNumber的算法

前置定理

推导D2
$$
\lfloor \frac{n}{d} \rfloor = \lceil \frac{n - d + 1}{d} \rceil\ and\ \lceil \frac {n}{d} \rceil = \lfloor \frac{n + d - 1}{d} \rfloor,\quad for\ d > 0
$$

$$
\lfloor \frac{n}{d} \rfloor = \lceil \frac{n - d - 1}{d} \rceil\ and\ \lceil \frac {n}{d} \rceil = \lfloor \frac{n + d + 1}{d} \rfloor,\quad for\ d < 0
$$

推导D4

如果$d \neq 0$，$x \in R$，则有：
$$
\lfloor \frac {n}{d} + x \rfloor = \lfloor \frac{n}{d} \rfloor\quad if\ 0 \leq x < |\frac{1}{d}|\
\lceil \frac {n}{d} + x \rceil = \lceil \frac{n}{d} \rceil\quad if\ -|\frac{1}{d}| < x \leq 0
$$

定义部分变量如下：

$n$: 被除数

$d$: 除数

$q$: 商

$r$: 余数

$M$: Magic Number

情况1：$d \geq 2$

设一个普通字的二进制位数为$W$，例如，32位整型的$W = 32$，则有$2 \leq d < 2^{W-1}$，我们希望找到一个最小的整数$m$和整数$p$使得

$$
\lfloor \frac{mn}{2^p} \rfloor = \lfloor \frac{n}{d} \rfloor, \quad for\ 0 \leq n < 2^{W - 1} \tag {1a}
$$

$$
\lfloor \frac{mn}{2^p} \rfloor + 1 = \lceil \frac{n}{d} \rceil, \quad for \ -2^{W - 1} \leq n \leq -1, \quad\ with\ 0 \leq m < 2^W \ and\ p \geq W \tag{1b}
$$

选用最小整数$m$的原因是，一个更小的乘数能够得到一个更小的移位数，同时$p \geq W$ 是因为生成的代码会在$mn$的低半部分产生移位，如32位情况下edx的内容就是乘法运算后右移32位的数据

注意到，Magic Number是实际参与乘法指令运算的数字，记为$M$, 其与算法中表述的$m$之间的关系为：
$$
\begin{equation}
M=
\begin{cases}
m, \quad\quad\quad\ \ if \ 0 \leq m < 2^{W - 1},\
m - 2^W, \quad if\ 2^{W - 1} \leq m < 2^W\
\end{cases}

\end{equation}
$$
由于公式(1b)必须满足$n = -d$，$\lfloor -md / 2^p \rfloor + 1 = -1$, 也就是：
$$
\frac{md}{2^p} > 1 \tag2
$$
令$n_c$为$n$的最大整数，并且$n_c \equiv d - 1(mod\ d)$，$n_c$一定存在因为有$n_c = d - 1$，且有
$$
n_c = \lfloor 2^{W - 1}/d \rfloor d- 1 = 2^{W - 1} - 2^{W - 1}mod\ d - 1
$$
同时，$n_c$是$n$的最大可接受值，因此有：
$$
2^{W - 1} - d \leq n_c\leq 2^{W - 1} - 1 \tag{3a}
$$

$$
n_c \geq d - 1 \tag{3b}
$$

由于公式(1a)必须满足$n = n_c$：
$$
\lfloor \frac{mn_c}{2^p} \rfloor = \lfloor \frac{n_c}{d} \rfloor = \frac{n_c - (d - 1)}{d}
$$
或者：
$$
\frac{mn_c}{2^p} < \frac{n_c + 1}{d}
$$
结合公式(2)有：
$$
\frac{2^p}{d} < m < \frac{2^p}{d} \frac{n_c + 1}{n_c} \tag4
$$
因为$m$是满足(4)式的最小整数, 它也是大于$2^p/d$的下一个整数，即：
$$
m = \frac{2^p + d - 2^p\ mod \ d}{d} \tag5
$$
结合此式和(4)式的右部有：
$$
2^p > n_c (d - 2^p\ mod\ d) \tag6
$$
由上述推导可知，该算法旨在找到Magic Number $M$ 和右移数$s$ 来计算$n_c$， 然后带入(6)式判断是否满足不等式，如果不满足则尝试更大的$p$和$n_c$。这里只讨论$p \geq W$的情况，该情况下，$m$可以通过(5)式直接计算得到

然而，如果$p$和$m$是通过(6)和(5)式计算得到的，那么它们必须满足式(1a)和(1b)，根据(4)式将$n$划分成以下5种情况：
$$
0 \leq n \leq n_c\
n_c + 1 \leq n \leq n_c + d - 1\
-n_c \leq n \leq -1\
-n_c - d + 1 \leq n \leq -n_c - 1\
n = -n_c - d
$$
根据式(4)，因为$m$为整数，有：
$$
\frac{2^p}{d} < m \leq \frac{2^p(n_c + 1) - 1}{dn_c}
$$
两边同时乘以$n/2^p$， 对于$n \geq 0$有：
$$
\frac{n}{d} \leq \frac{mn}{2^p} \leq \frac{2^p n(n_c + 1) - n}{2^p d n_c}
$$
因此有：
$$
\lfloor \frac{n}{d} \rfloor \leq \lfloor \frac{mn}{2^p}\rfloor \leq \lfloor \frac{n}{d} + \frac{(2^p - 1)n}{2^p d n_c} \rfloor
$$
对于$0 \leq n \leq n_c$，$0 \leq (2^p - 1)n/(2^p d n_c) < 1/d$， 根据D4有：
$$
\lfloor \frac{n}{d} + \frac{(2^p - 1)n}{2^p d n_c} \rfloor = \lfloor \frac{n}{d} \rfloor
$$
因此该情况下(1a)式满足

对于$n > n_c$， $n$被限制在范围：
$$
n_c + 1 \leq n \leq n_c + d - 1 \tag 9
$$
因为$n \geq n_c + d$ 和$n_c$的选择冲突，根据式(4)，对于$n\geq 0$,
$$
\frac{n}{d} < \frac{mn}{2^p} < \frac{n}{d} \frac{n_c + 1}{n_c}
$$
由四则运算推导得：
$$
\frac{n}{d} < \frac{mn}{2^p} < \frac{n_c + 1}{d} + \frac{(n - n_c)(n_c + 1)}{d n_c} \tag{10}
$$
根据(9)，$1\leq n - n_c \leq d - 1$，因此：
$$
0 < \frac{(n - n_c)(n_c + 1)}{d n_c} \leq \frac{d - 1}{d} \frac{n_c + 1}{n_c}
$$
因为$n_c > d - 1$ (3b) 并且 $(n_c + 1) / n_c $取最大值时$n_c$取最小值，因此有：
$$
0 < \frac{(n - n_c)(n_c + 1)}{d n_c} \leq \frac{d - 1}{d} \frac{d - 1 + 1}{d - 1} = 1
$$
在(10)式中，$(n_c + 1)/d$ 是一个整数，$(n - n_c)(n_c + 1)/d n_c$ 小于或者等于1， 因此(10)式变为：
$$
\lfloor \frac{n}{d} \rfloor \leq \lfloor \frac{mn}{2^p} \rfloor \leq \frac{n_c + 1}{d}
$$
对于(9)式中的$n$，$\lfloor n/d \rfloor = (n_c + 1)/d$，因此(1a)满足情况$(n_c + 1 \leq n \leq n_c + d - 1)$

对于$n < 0$, 从(4)式中我们有，因为$m$是一个整数，则：
$$
\frac{2^p + 1}{d} \leq m < \frac{2^p}{d} \frac{n_c + 1}{n_c}
$$
乘以$n/2^p$后，对于$n<0$有：
$$
\frac{n}{d} \frac{n_c + 1}{n_c} < \frac{mn}{2^p} \leq \frac{n}{d} \frac{2^p + 1}{2^p}
$$
或者：
$$
\lfloor \frac{n}{d} \frac{n_c + 1}{n_c} \rfloor + 1 < \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lfloor \frac{n}{d} \frac{2^p + 1}{2^p} \rfloor + 1
$$
根据D2推导得到：
$$
\lceil \frac{n(n_c + 1) - d n_c + 1}{d n_c} \rceil + 1 < \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lceil \frac{n(2^p + 1) - 2^p d + 1}{2^p d} \rceil + 1\
\lceil \frac{n(n_c + 1) + 1}{d n_c} \rceil < \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lceil \frac{n(2^p + 1) + 1}{2^p d} \rceil
$$
由于$n + 1 \leq 0$, 右边的不等式可以被缩放，有：
$$
\lceil \frac{n}{d} + \frac{n + 1}{d n_c} \rceil < \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lceil \frac{n}{d} \rceil
$$
对于 $-n_c \leq n \leq -1 $，
$$
\frac{-n_c + 1}{d n_c} \leq \frac{n + 1}{d n_c} \leq 0, or\
-\frac{1}{d} < \frac{n + 1}{d n_c} \leq 0
$$
因此根据D4有：
$$
\lceil \frac{n}{d} + \frac{n + 1}{d n_c} \rceil = \lceil \frac{n}{d} \rceil \tag{11}
$$
因此该情况下满足(1b)

对于$n < -n_c $, $n$被限制在范围：
$$
-n_c - d \leq n \leq - n_c - 1 \tag{12}
$$
从(3a)式可知，$n < -n_c - d$意味着$n < -2^{W - 1}$， 这是不可能的情况。对(11)式的左部进一步运算得到：
$$
\lceil \frac{-n_c - 1}{d} + \frac{(n + n_c)(n_c + 1) + 1}{d n_c} \rceil \leq \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lceil \frac{n}{d} \rceil \tag{13}
$$
对于$-n_c - d + 1 \leq n \leq -n_c - 1$，
$$
\frac{(-d + 1)(n_c + 1)}{d n_c} + \frac{1}{dn_c} \leq \frac{(n + n_c)(n_c + 1) + 1}{d n_c} \leq \frac{-(n_c + 1) + 1}{d n_c} = -\frac{1}{d}
$$
当$n_c$取最小值时，$(n_c + 1)/n_c$取最大值，即$n_c = d - 1$，因此有：
$$
\frac{(-d + 1)(d - 1 + 1)}{d(d-1)} + \frac{1}{d n_c} \leq \frac{(n + n_c)(n_c + 1) + 1}{d n_c} < 0, or\
-1 < \frac{(n + n_c)(n_c + 1) + 1}{d n_c} < 0
$$
对于(13)式，因为$(-n_c - 1)/d$是一个整数且它的增量在0到-1之间，则有：
$$
\frac{-n_c - 1}{d} \leq \lfloor \frac{mn}{2^p} \rfloor + 1 \leq \lceil \frac{n}{d} \rceil
$$
对于$-n_c - d + 1 \leq n \leq - n_c - 1$
$$
\lceil \frac{n}{d} \rceil = \frac{-n_c - 1}{d}
$$
因此，$\lfloor mn/2^p \rfloor + 1 = \lceil n/d \rceil $，(1b)式满足情况

对于最后一种情况，$n_c = -n_c - d$，只对部分$d$的值出现，由(3a)可知，$-n_c - d \leq -2^{W - 1}$，所以如果$n$取到这个值，我们一定有$n = -n_c - d = -2^{W - 1}$, 因此$n_c = 2^{W - 1} - d$, 因此，$2^{W - 1} \ mod\ d = (n_c + d)\ mod\ d = d - 1 $，即$d$除以$2^{W - 1} + 1$

对于$(n = -n_c - d)$, (6)式有解$p = W - 1$， 即$p$的最小可能值，
$$
n_c (d - 2^p\ mod\ d) = (2^{W - 1} - d)(d - 2^{W - 1}\ mod\ d)\
= (2^{W - 1} - d)(d - (d - 1)) = 2^{W - 1} - d < 2^{W - 1} = 2^p
$$
由(5)式有：
$$
m = \frac{2^{W - 1} +d - 2^{W - 1}\ mod\ d }{d} = \frac{2^{W - 1} + d - (d - 1)}{d} = \frac{2^{W - 1} + 1}{d}
$$
因此：
$$
\lfloor \frac{mn}{2^n} \rfloor +1 = \lfloor \frac{2^{W - 1} + 1}{d} \frac{-2^{W - 1}}{2^{W - 1}} \rfloor + 1 \= \lfloor \frac{-2^{W - 1} - 1}{d} \rfloor + 1
\= \lceil \frac{-2^{W - 1} - d}{d} \rceil + 1\ = \lceil \frac{-2^{W - 1}}{d} \rceil = \lceil \frac{n}{d} \rceil
$$
满足(1b)式

情况2：$d \leq -2$

因为有符号除法满足$n/(-d) = -n/d$，因此可以计算$n / |d|$来间接得到结果，但如果想要避免使用neg指令的话，也可以进行类似于情况1的推导

对于$W \geq 3$并且$-2^{W - 1} \leq d \leq -2$，我们希望找到在绝对值上最小的整数$m$和整数$p$使得：
$$
\lfloor \frac{mn}{2^p} \rfloor = \lfloor \frac{n}{d} \rfloor,\quad for\ -2^{W - 1} \leq n \leq 0 \tag{14a}
$$

$$
\lfloor \frac{mn}{2^n} \rfloor + 1 = \lceil \frac{n}{d} \rceil, \quad for\ 1 \leq n < 2^{W - 1} \tag{14b}
$$

$$
-2^W \leq m \leq 0, p \geq W
$$

令$n_c = kd + 1, k \in Z_+$, 此时$n_c$是对于$|d|$的可接受的$n$值，因此：
$$
-2^{W - 1} \leq n_c \leq -2^{W - 1} - d - 1 \tag{15a}
$$

$$
n_c \leq d + 1 \tag{15b}
$$

因为(14b)式必须满足$n = -d$, 且(14a)式必须满足$n = n_c$， 类似于(4)式有：
$$
\frac{2^p}{d} \frac{n_c - 1}{n_c} < m < \frac{2^p}{d} \tag{16}
$$
因为$m$式满足(16)式的最大整数，因此它是比$2^p/d$小的下一个整数，即：
$$
m = \frac{2^p - d - 2^p\ mod\ d}{d} \tag{17}
$$
结合此式和(16)式的左部有：
$$
2^p > n_c (d + 2^p\ mod\ d) \tag{18}
$$

最后，为了把运算限制在$W$字长内，需要做一些额外的处理

$n_c$能够通过下式计算得到：
$$
n_c =
\begin{cases}
2^{W - 1} - 2^{W - 1}\ mod\ d - 1, \quad\quad\ \ if \ d > 0,\
-2^{W - 1} - (2^{W - 1}+1)\ mod\ d, \quad if\ d < 0\
\end{cases}
$$
因此有：
$$
t = 2^{W - 1} + \begin{cases}
0,\quad if\ d > 0,\
1,\quad if\ d < 0
\end{cases}\ \tag{19}
|n_c| = t - 1 - t\ mod\ |d|
$$
由(6)式和(18)式，$p$能够通过下式得到：
$$
2^p > |n_c| (|d| - 2^p mod |d|)
$$
由(5)式和(17)式，$|m|$能够通过下式得到：
$$
|m| = \frac{2^p + |d| - 2^p\ mod\ |d|}{|d|}
$$
为了不使用双字长计算$2^p\ mod\ |d|$, 可以令$q, r$分别为$2^p / |d|, p = W - 1$的商和余数，并且$q, r$随着$p$的增加而更新，具体方法如下：

q = 2*q;
r = 2*r;
if(r >= abs(d)) {
    q = q + 1;
    r = r - abs(d);
}

由(4)式左部和(16)式右部以及$m$的范围可以得到$q = \lfloor 2^p/|d| \rfloor < 2^W$，此时$0\leq r < |d|$，两者都在$W$字长内

接下来，计算$\delta = |d| - r$，为了避免(19)式中的双字长乘法，将满足条件的式子重写为：
$$
\frac{2^p}{|n_c|} > \delta
$$
为了计算$m$, 有：
$$
\frac{2^p + |d| - 2^p\ mod\ |d|}{|d|} = \lfloor \frac{2^p}{|d|} \rfloor + 1 = q + 1
$$
假设只有$q_1, r_1$能够满足条件，则$2^p/|n_c| \leq \delta $可以表述为：
$$
q_1 < \delta\ |\ (q_1 = \delta\ &\ r_1 = 0)
$$
最后，把所有的情况汇总起来，算法可以写成如下形式：

struct ms {
    int M; // Magic Number
    int s; // shift amount
};

// 2 <= d <= 2**31 - 1 or -2**31 <= d <= -2
struct ms magic(int d)
{
    int p;
    unsigned ad, anc, delta, q1, r1, q2, r2, t;
    const unsigned two31 = 0x8000'0000; //2**31
    struct ms = mag;
    
    ad = abs(d);
    t = two31 + ((unsigned)d >> 31);
    anc = t - 1 - t%ad; // absolute value of nc
    p = 31;				// init p
    q1 = two31/anc;		// init q1 = 2**p / |nc|
    r1 = two31 - q1*anc;// init r1 = 2**p % |nc|
    q2 = two31/ad;		// init q2 = 2**p / |d|
    r2 = two31 - q2*ad; // init r2 = 2**p / |d|
    do
    {
        p = p + 1;
        q1 = 2*q1;		// update q1 = 2**p / |nc|
        r1 = 2*r1;		// update r1 = 2**p % |nc|
        if(r1 >= anc)	// must be an unsigned comparison
        {
            q1 = q1 + 1;
            r1 = r1 - anc;
        }
        a2 = 2*q2;		// update q2 = 2**p / |d|
        r2 = 2*r2;		// update r2 = 2**p % |d|
        if(r2 >= ad)	// must be an unsigned comparison
        {
            q2 = q2 + 1;
            r2 = r2 - ad;
        }
        delta = ad - r2;
    }while(q1 < delta || (q1 == delta && r1 == 0));
    mag.M = q2 + 1;
    if(d < 0)mag.M = -mag.M;
    mag.s = p - 32;
    return mag;
}