队列和广度优先搜索

队列和广度优先搜索

队列

队列是一种特殊的线性表，因为它只能从一端插入，一端删除，即先进先出的效果，类似于现实中的排队。

性质

  1. 先进先出
  2. 一般从队头入队，队尾出队
  3. 空队列：front = rear

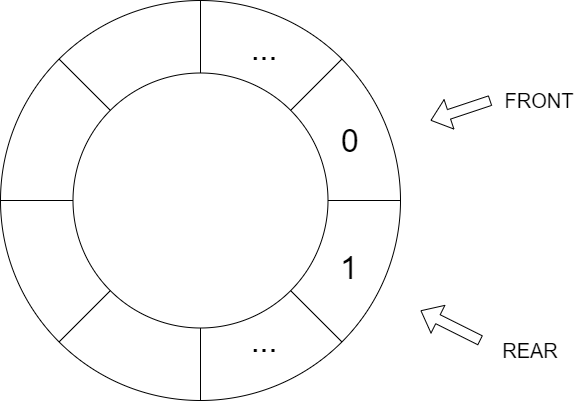
循环队列

由于队列中的元素只能从队头出，队尾进，因此如果不是特殊情况，采用顺序数组队列会浪费很多空间，并且它的使用也是有限制的（出队以后，队头之前的位置无法再被利用，而如果一直进队的话，数组总会被很快消耗完），因此可以考虑采用循环数组，将出队后的位置重新利用起来。

一般而言，循环队列的基本操作和特点如下：

  1. 队满：front = (rear + 1) % MAX_SIZE
  2. 队空：front = rear
  3. 插入元素：rear = (rear + 1) % MAX_SIZE
  4. 删除元素：front = (front + 1) % MAX_SIZE

其中MAX_SIZE是存放该队列的数组长度

img

队列为满时的情况

整体代码不算很难，但是要注意每次改变front 和 rear 的值时， 必须整除MAX_SIZE，以保证不会出现指针越界的情况。

代码如下（看看就好，跑不起来的）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//circle_queue.h
#define F(qu) (qu->front)
#define R(qu) (qu->rear)

typedef int ElemType;

#define MAX_SIZE 10   //定义最大队列长度

/** 
* 此队列中，头结点默认指向队列头部的元素，尾指针指向队列尾部元素的下一个空格
* 任何指针移动时，都必须要整除队列长度以保证不会越界
*/
typedef struct c_queue
{
    /* data */
    ElemType data[MAX_SIZE];
    int front;
    int rear;
}C_Queue;

C_Queue *init_circle_queue(C_Queue *qu);
int push(C_Queue *qu,ElemType *x);
int pop(C_Queue *qu);
int get_front(C_Queue *qu,ElemType *x);
int isfull(C_Queue *qu);
int isempty(C_Queue *qu);
void destory_circle_queue(C_Queue *qu);
void display(C_Queue *qu);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//circle_queue.c
#include "c_queue.h"

C_Queue *init_circle_queue(C_Queue *qu){
    qu = (C_Queue*)malloc(sizeof(C_Queue));
    qu->front = qu->rear = 0;
    return qu;
}

int isfull(C_Queue *qu){
    return qu->front == (qu->rear + 1) % MAX_SIZE;
}
int isempty(C_Queue *qu){
    return qu->front == qu->rear;
}

int push(C_Queue *qu,ElemType *x){
    if(isfull(qu)){
        perror("The queue is full!\n");
        return 0;
    }
    qu->data[qu->rear] = (*x);
    qu->rear = (qu->rear + 1) % MAX_SIZE;
    return 1;
}
int pop(C_Queue *qu){
    if(isempty(qu)){
        perror("The queue is empty!\n");
        return 0;
    }
    qu->front = (qu->front + 1) % MAX_SIZE;
    return 1;
}
int get_front(C_Queue *qu,ElemType *x){
    if(isempty(qu)){
        perror("The queue is empty!\n");
        return 0;
    }
    (*x) = qu->data[qu->front, MAX_SIZE];
    return 1;
}

void destory_circle_queue(C_Queue *qu){
    free(qu);
    return ;
}

void display(C_Queue *qu){
    int i = qu->front;
    while(i != qu->rear){
        printf("%d ", qu->data[i]);
        i = (i + 1) % MAX_SIZE;
    }
    return;
}

链式队列

链式队列的数据结构十分类似于链表，因此将链表加上头、尾指针后，就变成了链式队列。

基本操作

  1. 结点结构

    结点中包含需要存储的数据和下一个结点的指针就行。也可以将头尾结点指针包装起来。

  2. 插入

    先分析一般情况：当尾指针不为空时，直接将新结点插入到尾指针后面，再将尾指针指向这个新结点就好。

    当尾指针为空：此时队列中无元素，将头尾指针指向这个新结点就好。

  3. 删除

    也是先要分情况：当队列为空时，报错

    队列较长：先把头指针保留下来，将头指针后移，再释放原先的头指针。

    但是当队列只有一个元素时，最好还要保证尾指针不会变成野指针，因此做特殊情况处理，释放后将头尾指针指向空。

  4. 销毁队列

    先判断队列是否为空，若不为空则从头结点开始依次释放（可以调用删除函数，也可以循环）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//l_queue.h
typedef int ElemType;

typedef struct node{
    ElemType data;
    struct node *next;
}QNode;

typedef struct queue{
    QNode *front;
    QNode *rear;
}Queue;

Queue *init(Queue *qu);
int isempty(Queue *qu);
int push(Queue *qu, ElemType *x);
int pop(Queue *qu);
int get_front(Queue *qu, ElemType *x);
void destory_queue(Queue *qu);
void disp_queue(Queue *qu);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
//l_queue.c
#include "l_queue.h"

#define D(qu) (qu->data)
#define F(qu) (qu->front)
#define R(qu) (qu->rear)
#define N(qu) (qu->next)

Queue *init(Queue *qu){
    qu = (Queue*)malloc(sizeof(Queue));
    qu->front = qu->rear = NULL;
    return qu;
}

int isempty(Queue *qu){
    return qu->front == NULL;
}
int push(Queue *qu, ElemType *x){
    QNode *s = (QNode*)malloc(sizeof(QNode));
    s->next = NULL;
    s->data = (*x);
    if(R(qu) == NULL){
        F(qu) = R(qu) = s;
        return 1;
    }
    qu->rear->next = s;
    qu->rear = s;
    return 1;
}
int pop(Queue *qu){
    if(isempty(qu)){
        printf("The queue is empty!\n");
        return 0;
    }
    QNode *tmp = F(qu);
    if(F(qu) == R(qu)){
        free(F(qu));
        F(qu) = R(qu) = NULL;
    } else {
        F(qu) = N(F(qu));
        free(tmp);
    }
    return 1;
}
int get_front(Queue *qu, ElemType *x){
    if(isempty(qu)){
        printf("The queue is empty!\n");
        return 0;
    }  
    (*x) = D(F(qu));
    return 1;
}
void destory_queue(Queue *qu){
    while(F(qu) != NULL){
        pop(qu);
    }
    return ;
}

void disp_queue(Queue *qu){
    printf("queue:\n");
    if(F(qu) == NULL)return ;
    QNode *p = F(qu);
    while(p != R(qu)){
        printf("%d ", D(p));
        p = N(p);
    }
    printf("%d\n", D(p));
    return ;
}

广度优先搜索（BFS）

概念：广度优先搜索类似于一种横向式的搜索，对于它遇到的每一个合适的结点，都将放入考虑范围内，并且根据顺序依次访问，所以广度优先搜索常用于寻找最短路径。

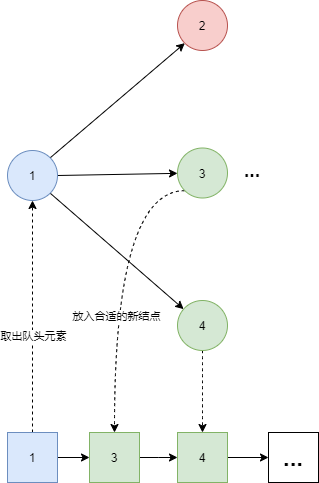
图结构中的BFS遍历

大致过程如下：首先访问初始点v，接着访问顶点v的所有未被访问过的邻接点v1，v2… 然后按照次序访问每一个未被访问过的顶点，直到找到所需要的顶点。由于始终优先访问最先被接触到的结点，因此适合用队列来实现。

通过下面的示意图能够很清晰的明白过程了。

bfs_gra


大致的代码思路如下（该代码需要图的基本算法）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//graph_basic.h

/** 
* 以邻接表的方式构建图
*/

typedef int ElemType;

#define MAX_SIZE 100

//声明边结点
typedef struct anode{
    //ElemType data;
    int vertex;
    struct anode *next;  //指向下一个边结点
    int weight;
}ANode;

//声明头结点
typedef struct vnode{
    ANode *firstarc;   //指向第一个边结点
    int isnode;
}VNode;

typedef struct graph{
    VNode adj_list[MAX_SIZE];   //邻接表
    int edges;
    int vertices;
}AdjGraph;

AdjGraph *init_with_file(AdjGraph *G, const char* filename); //使用文件来初始化图
void insert(AdjGraph *G, int u, int v, int w);  //插入结点
void destory_graph(AdjGraph *G);  //销毁表
void disp_adjlist(AdjGraph *G);  //显示邻接表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
//BFS.c

#include "graph_basic.h"
#include "l_queue.h"

//通过bfs寻找结点
void bfs(AdjGraph *G, int u, int v){
    //初始化容器
    Queue *qu = init(qu);
    int visited[MAX_SIZE] = {0};
    
    //添加首个结点到队列中
    push(qu, &u);
    visited[u] = 1;
    
    //处理队列中的每一个结点
    while(!isempty(qu)){
        int tmp;
        get_front(qu, &tmp);   //取出队列头部结点
        
        //找到答案，返回
        if(tmp == v){
            printf("find!\n");
            destory_queue(qu);
            return;
        }
        
        //在邻接表中寻找合适的结点
        ANode *p = G->adj_list[tmp].firstarc;
        while(p != NULL){
            int goal = p->vertex;
            if(visited[goal] == 0){
                visited[goal] = 1;
                push(qu, &goal);
            }
            p = p->next;
        }
        undel_pop(qu);   //当前结点处理完毕，从队列中弹出当前结点
    }
    printf("not find!\n");
    destory_queue(qu);
    return;
}

//寻找最短路径
void find_shortest_path(AdjGraph *G, int u, int v){
    //init
    Queue *qu = init(qu);
    int visited[MAX_SIZE] = {0};
    
    //处理首个结点
    push(qu, &u);
    visited[u] = 1;
    qu->front->parent = NULL;
    
    //处理队列中的结点
    while(!isempty(qu)){
        int tmp;
        get_front(qu, &tmp);  //取出头结点
        
        //找到目标则输出答案
        if(tmp == v){
            printf("find! Road:\n");
            QNode *t = qu->front;
            while(t->parent != NULL){
                printf("%d<-",t->data);
                t = t->parent;
            }
            printf("%d\n",t->data);
            destory_queue(qu);
            return;
        }
        
        //在邻接表中寻找合适的结点
        ANode *p = G->adj_list[tmp].firstarc;
        while(p != NULL){
            int goal = p->vertex;
            if(visited[goal] == 0){
                visited[goal] = 1;
                push(qu, &goal);
                qu->rear->parent = qu->front;
            }
            p = p->next;
        }
        
        undel_pop(qu);  //非删除式弹出结点，目的在于保留路径
    }
    
    //所有结点都遍历过了仍然没有找到
    printf("not find!\n");
    destory_queue(qu);
    return;
}

广义BFS

从广义上来说，BFS也是一种很常见的搜索方式，即处理完手里的所有情况之后，再去处理产生的新情况，下面是BFS寻找最小数值的伪代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
BFS function(params: root, target)
	init hash_table visited
	init a queue //storing the type of root
	init step = 0 //record minimum value from root to target
	add root to queue, visited
	//BFS
	while queue not empty:
		step++ //having walked one step
		init size = queue.size //the number of elements prepare to iterate next
		loop size times:
			init current node = queue.front
			if cur == target:
				return step
			else:
				for every suitable neighbors in cur: //most times mean not visited,not overedges and so on
					add each to queue, visited
			remove cur from queue
	//not found
	return -1
数据结构与算法
#BFS #队列
队列和广度优先搜索
http://example.com/2023/01/10/队列&广度优先搜索/
作者
Chen Shuwen
发布于
2023年1月10日
许可协议